The code for BiTree is trivial, as it simply delegates most calls to its state, the root node. The real work is done in the state. The code for EmptyNode and DatNode for the most part are equally trivial. The insertion and removal of the root data of a BiTree require some work and need some explanation. When does it make sense to remove the root node from a (binary) tree? That is, when can one unambiguously remove the root node from a binary tree?
Clearly, when both subtrees of a root node are non-empty, then removing the root node is problematic. However, it makes sense to allow root removal when at least one of the subtrees is empty. Suppose one of the subtrees is empty, then BiTree.remRoot() will change the state of this BiTree to the state of the other subtree. For example, when the left subtree is empty, root removal of the parent tree will set the parent tree to its right subtree.
The Best Tree Printing Algorithm in Texas
Consider the binary tree displayed in the following "horizontal" manner:
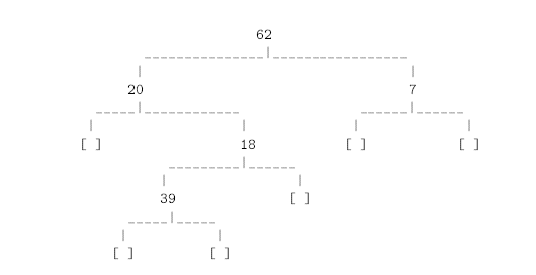
Such horizontal display of a tree is not very convenient when the tree is wide. It is more convenient to display the tree in a "vertical" manner.
The following visitor and its helper print the above tree "vertically" as shown below:
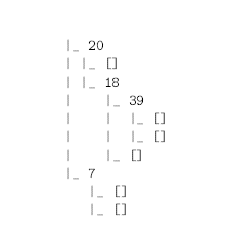
Let's study the algorithm.
- 2137 reads






