Exercise 2.5.1
Your friend Tracy argues: “It is bad to be depressed. Watching the news makes me feel depressed. Thus, it's good to avoid watching the news.”
Regardless of whether the premises and conclusion are true, show that the argument is not, by showing it doesn't hold for all domains. Replace "depressed" and
"watching news" with expressions which leave the premises true, but the conclusion false (or at least, what most reasonable people would consider false).
Exercise 2.5.2
An acquaintance says the following to you: " Chris claims knowledge is more important than grades. But she spent yesterday doing an extra-credit assignment which she already knew how to do.
Therefore, she's a hypocrite and deserves no respect. "
Regardless of whether the premises and conclusion are true, show that the argument is not, by showing it doesn't hold for all domains. Replace "knowledge" and
"grades" with expressions which give you true premises, but a false conclusion (or at least, what most reasonable people would consider false).
Exercise 2.5.3
While the following argument may sound plausible initially, give a particular situation where the conclusion doesn't hold (even though the premises do). Then, in a sentence or two, sketch why your counterexample may still represent rational behavior by pointing out a real-world subtlety that the initial argument ignored.
- If a certain outft meets a dress code, then peT foTce all less-revealing outfts also meet that dress code.
- In public transportation projects, out of two alternatives, the cheaper one which gets the job done is the better choice.
Exercise 2.5.4
Choose just one of the following informal arguments. While the argument sounds plausible initially, give a particular situation where the conclusion doesn't hold (even though the premises do). Then, briefy state why your counterexample may still represent rational behavior by pointing out a real-world subtlety that the initial argument ignored.
- [cell phone] Talking on a cell phone while driving increases the likelihood of an accident. Interestingly, hands-free phones do not signifcantly help29 . It's just the distraction of a phone conversation that causes the problem.
- [equivalent products] If two companies ofer two materially equivalent products, then most everybody will buy the cheaper one.
- [service] In a free market, if a company doesn't ofer good service, individual customers will become fed up and take their business elsewhere.
- [web browser] If there are two versions of a free web browser, and they run equally quickly, users will use the one with better featuresjinterface.
- [door-locking] Anybody who really wants to break into your house while you're gone will be able to. (For instance, using a towel to mufe sound, break the corner of a back window, reach in and unlatch the window, and climb through.) So there's no point in locking your front door.
Exercise 2.5.5
Let p, q, and r be the following propositions:- p: You get an A on the fnal exam
- q: You do every exercise in the book.
- r: You get an A in this class.
Write the following formulas using p, q, and r and logical connectives.
- You get an A in this class, but you do not do every exercise in the book.
- To get an A in this class, it is necessary for you to get an A on the fnal.
- Getting an A on the fnal and doing every exercise in the book is sufcient for getting an A in this class.
Exercise 2.5.6
Translate the following English sentences into propositional logic. Your answers should be WFFs.
- If the Astros win the series ("AW"), then pigs will fy ("PF").
- Pigs will not fy, andjor bacon will be free ("BF").
- The Astros will win the series, or bacon will be free, but not both.
Exercise 2.5.7
It just so happens that all the web pages in Logiconia which contain the word "Poppins" also contain the word "Mary". Write a formula (a query) expressing this. Use the proposition Poppins to represent the concept "the web page contains 'Poppins"' (and similar for Mary).
Exercise 2.5.8
- If a Logicanian page contains the word "weasel", then it also contains either "words" or "eyed"; and
- Whenever a Logiconian page contains the word "mongoose", it does not also contain the word "weasel"; and
- Finally, all Logiconian pages contain the word "Logiconia", rather patriotically.
Write a formula expressing all this. (Your formula will involve five propositions: weasel, words, ... Try to find a formula which mirrors the wording of the English
above.)
Given the above statements, if a web page in Logiconia does not contain "weasel", does it contain "mongoose"?
Let's go meta for a moment: Is this web page Logiconian? (Yes, this one you're looking at now, the one with the homework problems.) Explain why or why not.
Exercise 2.5.9
Different search engines on the web have their own syntax for speciflying searches.
ASIDE: Note that a formula may be true for some web pages, and false for others. The search engine is concerned with finding all web pages which satisfy the formula. This is called a
query, in database lingo.
Only a few allow full Boolean queries. Some interpret a list of several words in a row as an implicit conjunction, others as an implicit disjunctions.
- Read about the search syntax for the search language of eBay@3l . Write an eBay query for auctions which contain "border", do not contain "common", and contain at least one of "foreign" or "foriegn" [sic, misspellings are a great way to find underexposed auctions].
- Google£'s advanced search32 is typical for the online search engines. In particular, you can search for results containing all of a, b, ..., at least one of c, d, ..., and none of e, f, .... Describe how that corresponds to a Boolean formula.
- Give an example of a Boolean formula which cannot be rewritten to conform to Google's advanced search interface.
Exercise 2.5.10
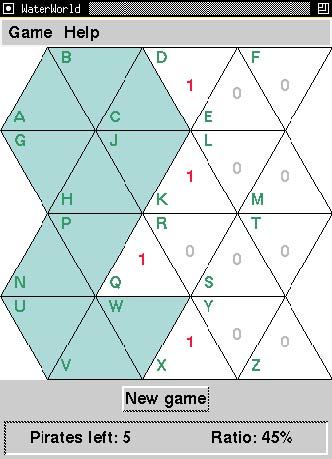
Consider the particular board shown in the above figure (Figure 2.7).
- Y − safe, Y − has − 0, and ¬Y − has − 2 are among the formulas which are true for this board but not for all boards. That is, they are neither domain axioms nor tautologies. Give two other such formulas.
- V − safe might or might not be true for this board. Give two other such formulas.
Exercise 2.5.11
In that same board (Figure 2.7), is location W safe? What is your informal reasoning? (List all your small steps.) Similarly for location P .
Exercise 2.5.12
Give a domain axiom of WaterWorld which was omitted in the ellipses in the WaterWorld domain axioms (Section 6.5).
Exercise 2.5.13
Even allowing for elision, the list of WaterWorld domain axioms (Section 6.5) is incomplete, in a sense. The game reports how many pirates exist in total, but that global information is not
reflected in the propositions or axioms.
First, assume we only use the default WaterWorld board size and number of pirates, i.e., five. Give samples of the additional axioms that we need.
Next, generalize your answer to model the program's ability to play the game with a different number of pirates.
Exercise 2.5.14
Give one WFF which meets all three conditions:
- true in all WaterWorld boards ("A theorem of WaterWorld")
- not already listed as one of the WaterWorld domain axioms (Propositional axioms for WaterWorld), and
- not a tautology of propositional logic (can be made false in some truth assignment, though it may not be a truth assignment which satisfies the WaterWorld axioms).
- 瀏覽次數:7260






