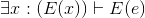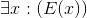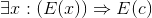您在這裡

首頁 » Intro to Logic » First-Order Logic » Exercises for First-Order Logic

Reasoning with Inference Rules

16 六月, 2015 - 17:13
Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/383d4b87-2d7b-454e-99fe-2eaa43eae8ff@20.20

Exercise 4.4.28

Prove that syllogisms are valid inferences. In other words, show that ∀x :
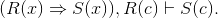
(R(x)\Rightarrow S(x)),R(c)\vdash S(c).

Exercise 4.4.29

What is wrong with the following "proof" of ∃x :(E (x)) ⇒ E (c)?

1

subproof:
\exists x:(E(x))\vdash E(e)

 

1.a

 

\exists x:(E(x))

Premise for subproof

1.b

 

E (c)

∃Elim, line 1.a

2

\exists x:(E(x))\Rightarrow E(c)

⇒Intro, line 1

Exercise 4.4.30

Using the inference rules, formally prove the last part of the previous problem about ducks and such (Exercise 4.4.11).

Exercise 4.4.31

Give an inference rule proof of ∀x : (Fruit (x) ⇒ hasMethod (tast y,x)) , ∀y : (Apple (y) ⇒ Fruit (y)) 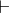\vdash∀z : (Apple (z) ⇒ hasMethod (tast y,z)).

Exercise 4.4.32

  1. Prove the following: ∃x :(P (x)) , ∀y :(P (y) ⇒ Q (y)) 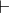\vdash∃z :(Q (z))
  2. Your proof above used ∃Intro. Why can't we replace that step with the formula ∀z :(Q (z)) with the justification "∀Intro"?
  3. Describe an interpretation which satisfies the proof's premises, but does not satisfy ∀z : (Q (z)).
  • 瀏覽次數：2828