Forall-Elim

Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/383d4b87-2d7b-454e-99fe-2eaa43eae8ff@20.20

Getting rid of universal quantifiers is easy: if you know ∀x :(φ) (where φ is a formula presumably involving x), well then you can replace x with anything you want, and the resulting formula will be true. We say
where t is any term. Any variables in t are arbitrary, unless it is an already-existing non-arbitrary variable.

For example, suppose we know that 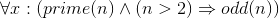We can replace n with some term like m+4 to conclud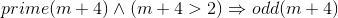e . The variable m is arbitrary, unless it already occurred in non-arbitrary in a previous line of the proof (perhaps introduced via ∃Elim). A more usual step is to use a term which is just a single variable, and (by coincidence) happens to have the same name as the quantified variable we are eliminating. Thus we often conclude 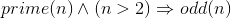 (note the absence of the initial ∀); n is arbitrary (unless it had already been confusingly in use as a non-arbitrary variable earlier). This is helpful when we'll be later re-introducing the ∀ in a later step; see the example below.