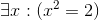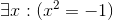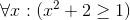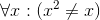Quantifiers

Exercise 4.4.8

Let P (x) be the statement "has been to Prague", where the domain consists of your classmates.

1. Express each of these quantifcations in English.
   • ∃x :(P (x))
   • ∀x :(P (x))
   • ¬∃x :(P (x))
   • ¬∀x :(P (x))
   • ∃x :(¬P (x))
   • ∀x :(¬P (x))
   • ¬∃x :(¬P (x))
   • ¬∀x :(¬P (x))
2. Which of these mean the same thing?

Exercise 4.4.9

Let C (x) be the statement "x has a cat", let D (x) be the statement "x has a dog", and let F (x) be the statement "x has a ferret". Express each of these statements in first-order logic using these relations. Let the domain be your classmates.

1. A classmate has a cat, a dog, and a ferret.
2. All your classmates have a cat, a dog, or a ferret.
3. At least one of your classmates has a cat and a ferret, but not a dog.
4. None of your classmates has a cat, a dog, and a ferret.
5. For each of the three animals, there is a classmate of yours that has one.

Exercise 4.4.10

Determine the truth value of each of these statements if the domain is all real numbers. Where appropriate, give a witness.