The relation nhbr, which we're defining as a set (of pairs), could also be thought of being a function. We say that the indicat or
function of a set is a Boolean function indicating whether its input is in the set or not. So instead of being given the set nhbr,
you would have been equally happy with its indicator function fnhbr, where (for example) fnhbr (B, C) = true and fnhbr (B, Q) = false. Similarly, if you know that fhasPirate (K) = true and that fhasPirate (L) =
false, then this is enough information to conclude that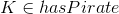 and
and 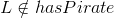 .
The set and the function are equivalent ways of modeling the same underlying relation.
.
The set and the function are equivalent ways of modeling the same underlying relation.
The next two exercises aren't meant to be difficult, but rather to illustrate that, while we've sketched these two approaches and suggested they are equivalent, we still need an exact definition.
Exercise 3.2.1
For the indicator function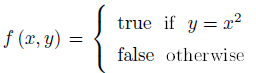 on the domain of (pairs of) natural numbers, write down the set-of-pairs representation for the corresponding binary relation. It's insightful to give the answer
both by listing the elements, possibly with ellipses, and also by using set-builder notation. In general, for a binary indicator function f, what, exactly, is the corresponding set?
on the domain of (pairs of) natural numbers, write down the set-of-pairs representation for the corresponding binary relation. It's insightful to give the answer
both by listing the elements, possibly with ellipses, and also by using set-builder notation. In general, for a binary indicator function f, what, exactly, is the corresponding set?
Exercise 3.2.2
For the relation hasPirate = {K, T, R, U, E} on the set of (individual) WaterWorld locations, write down the indicator-function representation for the corresponding unary relation. In general, how would you write down this translation?
Since these two formulations of a relation, sets and indicator functions, are so close, we'll often switch between them (a very slight abuse of terminology).
Think about when you write a program that uses the abstract data type Set. Its main operation is elementOf. When might you use an explicit enumeration to encode a set, and when an indicator function? Which would you use for the set of WaterWorld locations? Which for the set of prime numbers?
- 瀏覽次數:3479






