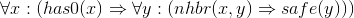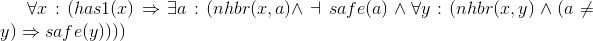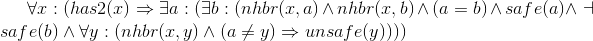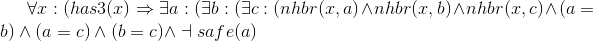Many of our axioms correspond directly, albeit much more succinctly, with those (Section 6.5.2: The domain axioms) of the propositional model. In addition, we have axioms that specify that our neighbor and equality relations are self-consistent.
Axioms asserting that the neighbor relation is anti-reflexive and symmetric:
- ∀x :(¬nhbr (x, x))
- ∀x :(∀y : (nhbr (x, y) ⇒ nhbr (y, x)))
Axioms asserting that "=" truly is an equality relation, i.e., it is reflexive, symmetric, and transitive.
- ∀x :(x = x)
- ∀x :(∀y : ((x = y) ⇒ (y = x)))
- ∀x :(∀y :(∀z : ((x = y) ∧ (y = z) ⇒ (x = z))))
Axioms asserting that the neighbor counts are correct. Each of these is of the form "if location x has n neighboring pirates, then there are n distinct unsafe neighbors of x, and any other distinct neighbor x is safe." We use the equality relation to specify the distinctness of each neighbor.
In addition, we want the implications to go the opposite way. Otherwise, each of has0, has1, has2, and has3 could always be false, while still satisfying the above! For brevity, we elide the details in the following list:
- ∀x :(∀y : (nhbr (x, y) ⇒ safe (y)) ⇒ has0 (x))
- ∀x :(... ⇒ has1 (x))
- ∀x :(... ⇒ has2 (x))
- ∀x :(... ⇒ has3 (x))
Axioms asserting that the neighbor counts are consistent. While redundant, including axioms like the following can be convenient.
- ∀x : (has0 (x) ⇒¬ (has1 (x) ∨ has2 (x) ∨ has3 (x)))
- ∀x : (has1 (x) ⇒¬ (has0 (x) ∨ has2 (x) ∨ has3 (x)))
- ∀x : (has2 (x) ⇒¬ (has0 (x) ∨ has1 (x) ∨ has3 (x)))
- ∀x : (has3 (x) ⇒¬ (has0 (x) ∨ has1 (x) ∨ has2 (x)))
Note that this set of axioms is not quite complete, as explored in an exercise (Exercise 4.4.22).
- 瀏覽次數:1917