Knowing the standard deviation is particularly important when the distribution of the scores falls on a normal distribution. When a standardized test is administered to a very large number of students the distribution of scores is typically similar, with many students scoring close to the mean, and fewer scoring much higher or lower than the mean. When the distribution of scores looks like the bell shape shown in Figure 12.7 (Bell shaped curve of normal distribution) it is called a normal distribution. In the diagram we did not draw in the scores of individual students as we did in Figure 12.8, because distributions typically only fall on a normal curve when there are a large number of students; too many to show individually. A normal distribution is symmetric, and the mean, median and mode are all the same.
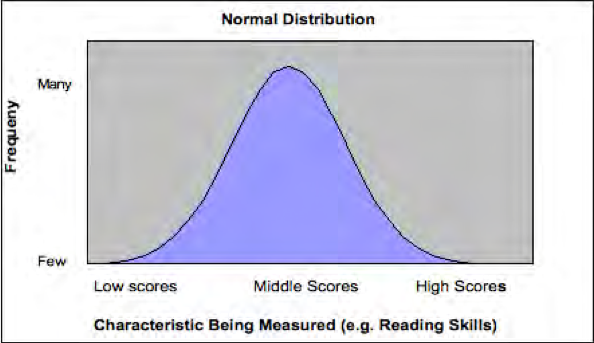
Normal curve distributions are very important in education and psychology because of the relationship between the mean, standard deviation, and percentiles. In all normal distributions 34 per cent of the scores fall between the mean and one standard deviation of the mean. Intelligence tests often are constructed to have a mean of 100 and standard deviation of 15 and we illustrate that in Figure 12.8.
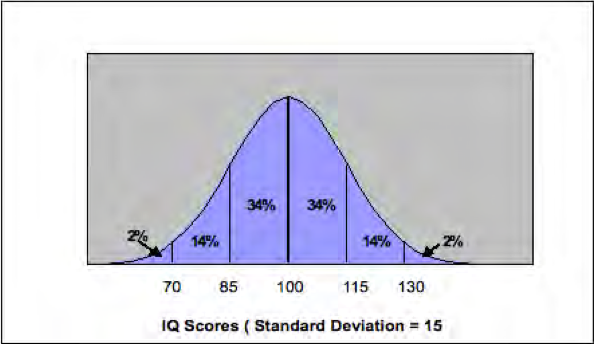
In this example, 34 per cent of the scores are between 100 and 115 and as well, 34 per cent of the scores lie between 85 and 100. This means that 68 per cent of the scores are between -1 and +1 standard deviations of the mean (i.e. 85 and 115). Note than only 14 per cent of the scores are between +1 and +2 standard deviations of the mean and only 2 per cent fall above +2 standard deviations of the mean.
In a normal distribution a student who scores the mean value is always in the fiftieth percentile because the mean and median are the same. A score of +1 standard deviation above the mean (e.g. 115 in the example above) is the 84 per cent tile (50 per cent and 34 per cent of the scores were below 115). In Figure 12.9 we represent the percentile equivalents to the normal curve and we also show standard scores. 1
- 8803 reads






