A dollar earned today is worth more than a dollar earned one or more years from now. The NPV of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present values (PVs) of the individual cash flows of the same entity.
In the case when all future cash flows are incoming and the only outflow of cash is the purchase price, the NPV is simply the PV of future cash flows minus the purchase price (which is its own PV). NPV is a standard method for using the time value of money to appraise long-term projects. Used for capital budgeting and widely used throughout economics, finance, and accounting, it measures the excess or shortfall of cash flows, in present value terms, once financing charges are met.
NPV can be described as the “difference amount” between the sums of discounted cash inflows and cash outflows. It compares the present value of money today to the present value of money in the future, taking inflation and returns into account.
The NPV of a sequence of cash flows takes as input the cash flows and a discount rate or discount curve and outputs a price.
Each cash inflow/outflow is discounted back to its present value (PV). Then they are summed. Therefore NPV is the sum of all terms.
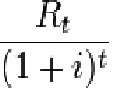
where
tis the time of the cash flow
iis the discount rate (the rate of return that could be earned on an investment in the financial markets with similar risk; the opportunity cost of capital)
Rtis the net cash flow (i.e., cash inflow – cash outflow, at time t).
NPV is an indicator of how much value an investment or project adds to the firm. With a particular project, if NPV is a positive value, the project is in the status of positive cash inflow in the time t. If NPV is a negative value, the project is in the status of discounted cash outflow in the time t. Sometimes risky projects with a positive NPV could be accepted. This does not necessarily mean that they should be undertaken since NPV at the cost of capital may not account for opportunity cost (i.e., comparison with other available investments). In financial theory, if there is a choice between two mutually exclusive alternatives, the one yielding the higher NPV should be selected.
|
If… |
It means… |
Then… |
|---|---|---|
|
NPV>0 |
The investment would add value to the firm |
The project may be accepted |
|
NPV<0 |
The investment would subtract value from the firm |
The project should be rejected |
|
NPV=0 |
The investment would neither gain nor lose value for the firm |
We should be indifferent in the decision whether to accept or reject the project. This project adds no monetary value. Decision should be based on other criteria (e.g, strategic positioning or other factors not explicitly included in the calculation). |
Present Value Table
|
Periods |
6% |
8% |
10% |
12% |
14% |
|---|---|---|---|---|---|
|
1 |
0.943 |
0.926 |
0.909 |
0.893 |
0.877 |
|
2 |
0.890 |
0.857 |
0.826 |
0.797 |
0.769 |
|
3 |
0.840 |
0.794 |
0.751 |
0.712 |
0.675 |
|
4 |
0.792 |
0.735 |
0.683 |
0.636 |
0.592 |
|
5 |
0.747 |
0.681 |
0.621 |
0.567 |
0.519 |
|
6 |
0.705 |
0.630 |
0.564 |
0.507 |
0.456 |
|
7 |
0.665 |
0.583 |
0.513 |
0.452 |
0.400 |
|
8 |
0.627 |
0.540 |
0.467 |
0.404 |
0.351 |
|
9 |
0.592 |
0.500 |
0.424 |
0.361 |
0.308 |
|
10 |
0.558 |
0.436 |
0.386 |
0.322 |
0.270 |
- 2797 reads






