Example 4.6

Available under Creative Commons-ShareAlike 4.0 International License.

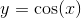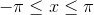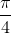Calculate $y=\textrm{cos}(x)$ for $-\pi \leq x\leq \pi$ using an increment of $\frac{\pi }{4}$ .

for x=-pi:pi/4:pi
    y=cos(x);
    fprintf('%8.3f %8.2f nn',x,y);
end

In the brief script above, x is the loop index that is initiated from 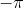$-\pi$ and incremented with 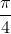$\frac{\pi }{4}$ to a ﬁnal value of 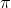$\pi$ . At the end of each increment, 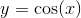$y=\textrm{cos}(x)$ is calculated and displayed with the fprintf command. This process continues until $x=\pi$ .

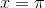From a previous exercise we know \n creates a new line when included in the fprintf command. Here, we also use %8.3f to specify eight spaces and three decimal places for the ﬁrst variable x. Likewise %8.2f speciﬁes the formatting for the second variable y but in this case, y is displayed with two decimal places. The result is the following:

-3.142  -1.00
-2.356  -0.71
-1.571   0.00
-0.785   0.71
0.000    1.00
0.785    0.71
1.571    0.00
2.356   -0.71
3.142   -1.00

We can improve our code by adding formatting lines as follows:

clear; clc;
fprintf(' x cos(x)nn') % title row
fprintf(' ----------------nn') % title row
    for x=-pi:pi/4:pi % loop_index=inital_value:increment_value:final_value
        y=cos(x); % code to calculate cos(x)
        fprintf('%8.3f %8.2f nn',x,y); % code to print the output to screen
end

Screen output:

x           cos(x)
----------------
-3.142     -1.00
-2.356     -0.71
-1.571      0.00
-0.785      0.71
0.000       1.00
0.785       0.71
1.571       0.00
2.356      -0.71
3.142      -1.00

瀏覽次數：1226

您在這裡

Example 4.6