Suppose we calculate some variable of interest, y, as a function of some other variable x. We call y the dependent variable and x the independent variable. For example, consider the data set below, taken from a simple experiment involving a vehicle, its velocity versus time is tabulated. In this case, velocity is a function of time, thus velocity is the dependent variable and the time is the independent variable.
|
Time [s] |
Velocity [m/s] |
|
0 |
20 |
|
10 |
39 |
|
20 |
67 |
|
30 |
89 |
|
40 |
111 |
|
50 |
134 |
|
60 |
164 |
|
70 |
180 |
|
80 |
200 |
In its simplest form regression analysis involves fitting the best straight line relationship to explain how the variation in a dependent variable, y, depends on the variation in an independent variable, x. In our example above, once the relationship (in this case a linear relationship) has been estimated we can produce a linear equation in the following form:
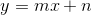
And once an analytic equation such as the one above has been determined, dependent variables at intermediate independent values can be computed.
- 瀏覽次數:1859






