The actual test begins by considering two hypotheses. They are called the null hypothesis and the alternate hypothesis. These hypotheses contain opposing viewpoints.
Ho: The null hypothesis: It is a statement about the population that will be assumed to be true unless it can be shown to be incorrect beyond a reasonable doubt.
Ha: The alternate hypothesis: It is a claim about the population that is contradictory to Ho and what we conclude when we reject Ho.
Example 5.1
Ho: No more than 30% of the registered voters in Santa Clara County voted in the primary election.
Ha: More than 30% of the registered voters in Santa Clara County voted in the primary election.
Example 5.2
We want to test whether the mean grade point average in American colleges is different from 2.0 (out of 4.0).

Example 5.3
We want to test if college students take less than five years to graduate from college, on the average.

Example 5.4
In an issue of U. S. News and World Report, an article on school standards stated that about half of all students in France, Germany, and Israel take advanced
placement exams and a third pass. The same article stated that 6.6% of U. S. students take advanced placement exams and 4.4 % pass. Test if the percentage of U. S. students who take advanced
placement exams is more than 6.6%.

Since the null and alternate hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject Ho" if the sample information favors the alternate hypothesis or "do not reject Ho" or "fail to reject Ho" if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in Ho and Ha:
|
Ho |
Ha |
|---|---|
|
equal (=) |
not equal ( |
|
greater than or equal to (≥) |
less than (<) |
|
less than or equal to (≤) |
more than (>) |
- 瀏覽次數:3378





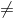 ) or greater than (>)
or less than (<)
) or greater than (>)
or less than (<)

