Changing the Confidence Level or Sample Size

Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/733d1554-5d75-4798-9e54-7dcdc1ee5690@5.40

Example 4.3: Changing the Confidence Level

Suppose we change the original problem by using a 95% confidence level. Find a 95% confidence interval for the true (population) mean statistics exam score.

Solution
To find the confidence interval, you need the sample mean, 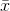$\bar{x}$ , and the EBM.
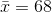
$\bar{x}=68$
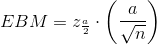
$EBM=z_{\frac{a}{2}}\cdot \left ( \frac{a}{\sqrt{n}} \right )$
σ =3 ; n = 36 ; The confidence level is 95% (CL = 0.95)
CL = 0.95 so α = 1 − CL = 1 − 0.95 = 0.05

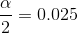
$\frac{\alpha }{2}=0.025$
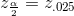
$z_{\frac{\alpha }{2}}=z_{.025}$
The area to the right of z_.025 is 0.025 and the area to the left of z_.025 is 1−0.025 = 0.975
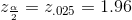
$z_{\frac{\alpha }{2}}= z_{.025} =1.96$
using invnorm(.975,0,1) on the TI-83,83+,84+ calculators. (This can also be found using appropriate commands on other calculators, using a computer, or using a probability table for the Standard Normal distribution.)
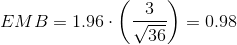
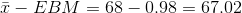
$EMB=1.96\cdot \left ( \frac{3}{\sqrt{36}} \right )=0.98$ $\bar{x}-EBM=68-0.98=67.02$
$\bar{x}+EBM=68+0.98=68.98$

Interpretation

We estimate with 95% confidence that the true population mean for all statistics exam scores is between 67.02 and 68.98.

Explanation of 95% Confidence Level

95% of all confidence intervals constructed in this way contain the true value of the population mean statistics exam score.

Comparing the results

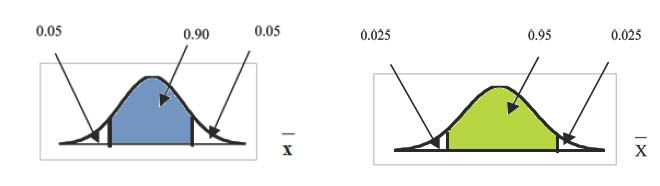
The 90% confidence interval is (67.18, 68.82). The 95% confidence interval is (67.02, 68.98). The 95% confidence interval is wider. If you look at the graphs, because the area 0.95 is larger than the area 0.90, it makes sense that the 95% confidence interval is wider.

Figure 4.1 Comparing the results

Summary: Effect of Changing the Confidence Level

Increasing the confidence level increases the error bound, making the confidence interval wider.
Decreasing the confidence level decreases the error bound, making the confidence interval narrower.

Example 4.4: Changing the Sample Size:

Suppose we change the original problem to see what happens to the error bound if the sample size is changed.

See the following Problem.

Problem

Leave everything the same except the sample size. Use the original 90% confidence level. What happens to the error bound and the confidence interval if we increase the sample size and use n=100 instead of n=36? What happens if we decrease the sample size to n=25 instead of n=36?

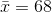
$\bar{x}=68$
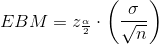
$EBM=z_{\frac{\alpha }{2}}\cdot \left ( \frac{\sigma}{\sqrt{n}} \right )$
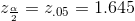
σ = 3 ; The confidence level is 90% (CL = 0.90) ; $z_{\frac{\alpha }{2}}=z_{.05}=1.645$

Solution A
If we increase the sample size n to 100, we decrease the error bound.
When n = 100 : 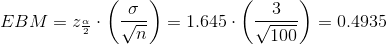$EBM=z_{\frac{\alpha }{2}}\cdot \left ( \frac{\sigma }{\sqrt{n}} \right )=1.645\cdot \left ( \frac{3}{\sqrt{100}} \right )=0.4935$

Solution B
If we decrease the sample size n to 25, we increase the error bound.
When n = 25 :
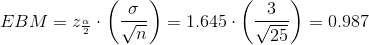
$EBM=z_{\frac{\alpha }{2}}\cdot \left ( \frac{\sigma }{\sqrt{n}} \right )=1.645\cdot \left ( \frac{3}{\sqrt{25}} \right )=0.987$

Summary: Effect of Changing the Sample Size

Increasing the sample size causes the error bound to decrease, making the confidence interval narrower.
Decreasing the sample size causes the error bound to increase, making the confidence interval wider.

84493 reads

You are here

Changing the Confidence Level or Sample Size