Working Backwards to find the Error Bound or the Sample Mean
When we calculate a confidence interval, we find the sample mean and calculate the error bound and use them to calculate the confidence interval. But sometimes when we read statistical studies, the study may state the confidence interval only. If we know the confidence interval, we can work backwards to find both the error bound and the sample mean.
Finding the Error Bound
- From the upper value for the interval, subtract the sample mean
- OR, From the upper value for the interval, subtract the lower value. Then divide the diference by 2.
Finding the Sample Mean
- Subtract the error bound from the upper value of the confidence interval
- OR, Average the upper and lower endpoints of the confidence interval
Notice that there are two methods to perform each calculation. You can choose the method that is easier to use with the information you know.
Example 4.5
Suppose we know that a confidence interval is (67.18, 68.82) and we want to find the error bound.
We may know that the sample mean is 68. Or perhaps our source only gave the confidence interval and did not tell us the value of the the sample mean.
Calculate the Error Bound:
- If we know that the sample mean is 68: EBM = 68.82 − 68 = 0.82
- If we don't know the sample mean:
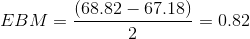
Calculate the Sample Mean:
- If we know the error bound:
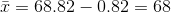
- If we don't know the error bound:
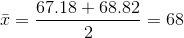
- 56752 reads






