Linear regression for two variables is based on a linear equation with one independent variable. It has the form:
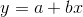
where a and b are constant numbers.
x is the independent variable, and y is the dependent variable. Typically, you choose a value to substitute for the independent variable and then solve for the dependent variable.
Example 6.1
The following examples are linear equations.
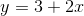
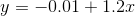
The graph of a linear equation of the form y = a + bx is a straight line. Any line that is not vertical can be described by this equation.
Example 6.2
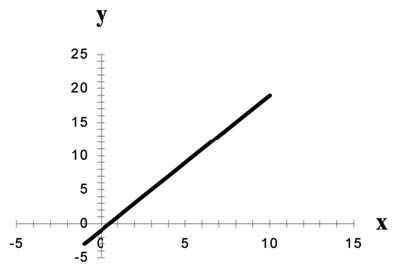
Linear equations of this form occur in applications of life sciences, social sciences, psychology, business, economics, physical sciences, mathematics, and other areas.
Example 6.3
Aaron's Word Processing Service (AWPS) does word processing. Its rate is $32 per hour plus a $31.50 one-time charge. The total cost to a customer depends on the number of hours it takes to do
the word processing job.
See the following Problem.
Problem
Find the equation that expresses the total cost in terms of the number of hours required to finish the word processing job.
Solution
Let x = the number of hours it takes to get the job done.
Let y = the total cost to the customer.
The $31.50 is a fixed cost. If it takes x hours to complete the job, then (32) (x) is the cost of the word processing only. The total cost is:
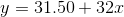
- 4256 reads






