Suppose you are trying to determine the mean rent of a two-bedroom apartment in your town. You might look in the classified section of the newspaper, write down several rents listed, and average them together. You would have obtained a point estimate of the true mean. If you are trying to determine the percent of times you make a basket when shooting a basketball, you might count the number of shots you make and divide that by the number of shots you attempted. In this case, you would have obtained a point estimate for the true proportion.
We use sample data to make generalizations about an unknown population. This part of statistics is called inferential statistics. The sample data help us to make an estimate of a population parameter. We realize that the point estimate is most likely not the exact value of the population parameter, but close to it. After calculating point estimates, we construct confidence intervals in which we believe the parameter lies.
In this chapter, you will learn to construct and interpret confidence intervals. You will also learn a new distribution, the Student's-t, and how it is used with these intervals. Throughout the chapter, it is important to keep in mind that the confidence interval is a random variable. It is the parameter that is fixed.
If you worked in the marketing department of an entertainment company, you might be interested in the mean number of compact discs (CD's) a consumer buys per month. If so, you could conduct a
survey and calculate the sample mean, 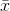 , and the sample standard
deviation, s. You would use
, and the sample standard
deviation, s. You would use 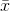 to estimate the population mean
and s to estimate the population standard deviation. The sample mean,
to estimate the population mean
and s to estimate the population standard deviation. The sample mean, 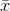 , is the point estimate for the population mean, µ. The sample standard deviation, s, is the point estimate
for the population standard deviation, σ.
, is the point estimate for the population mean, µ. The sample standard deviation, s, is the point estimate
for the population standard deviation, σ.
Each of 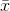 and s is also called a statistic.
and s is also called a statistic.
A confidence interval is another type of estimate but, instead of being just one number, it is an interval of numbers. The interval of numbers is a range of values calculated from a given set of sample data. The confidence interval is likely to include an unknown population parameter.
Suppose for the CD example we do not know the population mean µ but we do know that the population standard deviation is σ =1 and our sample size is 100. Then by the Central Limit Theorem, the standard deviation for the sample mean is
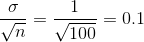
The Empirical Rule, which applies to bell-shaped distributions, says that in approximately 95% of the samples, the sample mean, 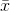 , will be within two standard deviations of the population mean µ. For our CD example, two
standard deviations is (2) (0.1) = 0.2. The sample mean
, will be within two standard deviations of the population mean µ. For our CD example, two
standard deviations is (2) (0.1) = 0.2. The sample mean 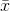 is likely
to be within 0.2 units of µ.
is likely
to be within 0.2 units of µ.
Because 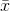 is within 0.2 units of µ, which is unknown, then µ is
likely to be within 0.2 units of
is within 0.2 units of µ, which is unknown, then µ is
likely to be within 0.2 units of 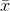 in 95% of the samples. The
population mean µ is contained in an interval whose lower number is calculated by taking the sample mean and subtracting two standard deviations ((2) (0.1)) and whose upper number is calculated
by taking the sample mean and adding two standard deviations. In other words, µ is between
in 95% of the samples. The
population mean µ is contained in an interval whose lower number is calculated by taking the sample mean and subtracting two standard deviations ((2) (0.1)) and whose upper number is calculated
by taking the sample mean and adding two standard deviations. In other words, µ is between 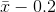 and
and 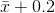 in 95% of all the samples.
in 95% of all the samples.
For the CD example, suppose that a sample produced a sample mean 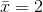 . Then the unknown population mean µ is between
. Then the unknown population mean µ is between
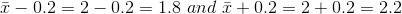
We say that we are 95% confident that the unknown population mean number of CDs is between 1.8 and 2.2. The 95% confidence interval is (1.8, 2.2).
The 95% confidence interval implies two possibilities. Either the interval (1.8, 2.2) contains the true mean µ or our sample produced an 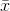 that is not within 0.2 units of the true mean µ. The second possibility happens for only 5%
of all the samples (100% - 95%).
that is not within 0.2 units of the true mean µ. The second possibility happens for only 5%
of all the samples (100% - 95%).
Remember that a confidence interval is created for an unknown population parameter like the population mean, µ. Confidence intervals for some parameters have the form
(point estimate - margin of error, point estimate + margin of error)
The margin of error depends on the confidence level or percentage of confidence.
When you read newspapers and journals, some reports will use the phrase "margin of error." Other reports will not use that phrase, but include a confidence interval as the point estimate + or - the margin of error. These are two ways of expressing the same concept.
- 2171 reads






