Normal Distribution: Standard Normal Distribution

Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/733d1554-5d75-4798-9e54-7dcdc1ee5690@5.40

The standard normal distribution is a normal distribution of standardized values called z-scores. A z-score is measured in units of the standard deviation. For example, if the mean of a normal distribution is 5 and the standard deviation is 2, the value 11 is 3 standard deviations above (or to the right of) the mean. The calculation is:

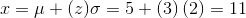
$x=\mu +(z)\sigma =5+\left ( 3 \right )\left ( 2 \right )=11$

The z-score is 3.

The mean for the standard normal distribution is 0 and the standard deviation is 1. The transformation 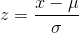$z=\frac{x-\mu }{\sigma }$ produces the distribution Z∼ N (0, 1) . The value x comes from a normal distribution with mean µ and standard deviation σ.

1603 reads

You are here

Normal Distribution: Standard Normal Distribution