r2 is called the coefficient of determination. r2 is the square of the correlation coefficient, but is usually stated as a percent, rather than in decimal form. r2 has an interpretation in the context of the data:
- r2, when expressed as a percent, represents the percent of variation in the dependent variable y that can be explained by variation in the independent variable x using the regression (best fit) line.
- 1-r2, when expressed as a percent, represents the percent of variation in y that is NOT explained by variation in x using the regression line. This can be seen as the scattering of the observed data points about the regression line.
Consider the third exam/final exam example introduced in the previous section
The line of best fit is: 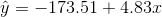
The correlation coefficient is r = 0.6631
The coefficient of determination is r2 = 0.66312 = 0.4397
Interpretation of r2 in the context of this example:
Approximately 44% of the variation (0.4397 is approximately 0.44) in the final exam grades can be explained by the variation in the grades on the third exam, using the best fit regression line.
Therefore approximately 56% of the variation (1 - 0.44 = 0.56) in the fnal exam grades can NOT be explained by the variation in the grades on the third exam, using the best fit regression line. (This is seen as the scattering of the points about the line.)
**With contributions from Roberta Bloom.
- 3626 reads






