A
Average
A number that describes the central tendency of the data. There are a number of specialized averages, including the arithmetic mean, weighted mean, median, mode, and geometric mean.
B
Binomial Distribution
A discrete random variable (RV) which arises from Bernoulli trials. There are a fixed number, n, of independent trials. "Independent" means that the result of any trial (for example,
trial 1) does not affect the results of the following trials, and all trials are conducted under the same conditions. Under these circumstances the binomial RV X is defined as the number of successes in n trials. The notation is: X∼B (n,
p). The mean is µ = np and the standard deviation is 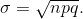 The probability of exactly x successes in n trials is
The probability of exactly x successes in n trials is 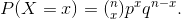
C
Central Limit Theorem
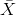 , and the sample sum, ΣX. If the size n
of the sample is sufficiently large, then
, and the sample sum, ΣX. If the size n
of the sample is sufficiently large, then 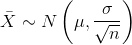 and
and 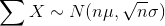 . If the size n of the sample is sufciently large, then the distribution of the sample means and the distribution of the sample sums
will approximate a normal distribution regardless of the shape of the population. The mean of the sample means will equal the population mean and the mean of the sample sums will equal n times
the population mean. The standard deviation of the distribution of the sample means,
. If the size n of the sample is sufciently large, then the distribution of the sample means and the distribution of the sample sums
will approximate a normal distribution regardless of the shape of the population. The mean of the sample means will equal the population mean and the mean of the sample sums will equal n times
the population mean. The standard deviation of the distribution of the sample means, 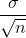 , is called the standard error of the mean.
, is called the standard error of the mean.
Coefficient of Correlation
A measure developed by Karl Pearson (early 1900s) that gives the strength of association between the independent variable and the dependent variable. The formula is:
![r=\frac{n\sum xy -(\sum x)(\sum y)}{\sqrt{[n\sum x^{2}-(\sum x)^{2}][n\sum y^{2}-(\sum y)^{2}]}}](/system/files/resource/9/9418/9502/media/eqn-img_31.gif)
where n is the number of data points. The coefficient cannot be more then 1 and less then -1. The closer the coefficient is to ±1, the stronger the evidence of a significant linear relationship between x and y.
Confidence Interval (CI)
An interval estimate for an unknown population parameter. This depends on:
- The desired confidence level.
- Information that is known about the distribution (for example, known standard deviation).
- The sample and its size.
Confidence Level (CL)
The percent expression for the probability that the confidence interval contains the true population parameter. For example, if the CL = 90%, then in 90 out of 100 samples the interval estimate will enclose the true population parameter.
Continuous Random Variable
A random variable (RV) whose outcomes are measured.
Example: The height of trees in the forest is a continuous RV.
Cumulative Relative Frequency
The term applies to an ordered set of observations from smallest to largest. The Cumulative Relative Frequency is the sum of the relative frequencies for all values that are less than or equal to the given value.
D
Data
A set of observations (a set of possible outcomes). Most data can be put into two groups: qualitative (hair color, ethnic groups and other attributes of the population) and quantitative (distance traveled to college, number of children in a family, etc.). Quantitative data can be separated into two subgroups: discrete and continuous. Data is discrete if it is the result of counting (the number of students of a given ethnic group in a class, the number of books on a shelf, etc.). Data is continuous if it is the result of measuring (distance traveled, weight of luggage, etc.)
Degrees of Freedom (df)
The number of objects in a sample that are free to vary.
Discrete Random Variable
A random variable (RV) whose outcomes are counted.
E
Error Bound for a Population Mean (EBM)
The margin of error. Depends on the confidence level, sample size, and known or estimated population standard deviation.
Error Bound for a Population Proportion(EBP)
The margin of error. Depends on the confidence level, sample size, and the estimated (from the sample) proportion of successes.
Exponential Distribution
A continuous random variable (RV) that appears when we are interested in the intervals of time between some random events, for example, the length of time between emergency arrivals at a
hospital. Notation: X~Exp (m). The mean is 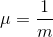 and the standard deviation is
and the standard deviation is 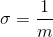 . The probability density function is f(x) = me-mx , x ≥ 0 and the cumulative distribution
function is P (X ≤ x) = 1 – e-mx.
. The probability density function is f(x) = me-mx , x ≥ 0 and the cumulative distribution
function is P (X ≤ x) = 1 – e-mx.
F
Frequency
The number of times a value of the data occurs.
H
Hypothesis
A statement about the value of a population parameter. In case of two hypotheses, the statement assumed to be true is called the null hypothesis (notation H0) and the contradictory statement is called the alternate hypothesis (notation Ha).
Hypothesis Testing
Based on sample evidence, a procedure to determine whether the hypothesis stated is a reasonable statement and cannot be rejected, or is unreasonable and should be rejected.
I
Inferential Statistics
Also called statistical inference or inductive statistics. This facet of statistics deals with estimating a population parameter based on a sample statistic. For example, if 4 out of the 100 calculators sampled are defective we might infer that 4 percent of the production is defective.
L
Level of Significance of the Test
Probability of a Type I error (reject the null hypothesis when it is true). Notation: α. In hypothesis testing, the Level of Significance is called the preconceived α or the preset α.
M
Mean
A number that measures the central tendency. A common name for mean is 'average.' The term 'mean' is a shortened form of 'arithmetic mean.' By definition, the mean for a sample (denoted by
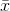 ) is
) is 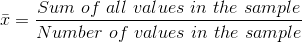 , and the mean for a population (denoted by µ) is
, and the mean for a population (denoted by µ) is 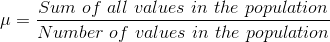 .
.
Median
A number that separates ordered data into halves. Half the values are the same number or smaller than the median and half the values are the same number or larger than the median. The median may or may not be part of the data.
Mode
The value that appears most frequently in a set of data.
N
Normal Distribution
A continuous random variable (RV) with pdf 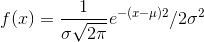 , where µ is the mean of the distribution and σ is the standard deviation. Notation: X ∼ N (µ, σ). If µ =0 and σ =1, the RV is called the standard normal distribution.
, where µ is the mean of the distribution and σ is the standard deviation. Notation: X ∼ N (µ, σ). If µ =0 and σ =1, the RV is called the standard normal distribution.
P
p-value
The probability that an event will happen purely by chance assuming the null hypothesis is true. The smaller the p-value, the stronger the evidence is against the null hypothesis.
Parameter
A numerical characteristic of the population.
Point Estimate
A single number computed from a sample and used to estimate a population parameter.
Population
The collection, or set, of all individuals, objects, or measurements whose properties are being studied.
Proportion
- As a number: A proportion is the number of successes divided by the total number in the sample.
- As a probability distribution: Given a binomial random variable (RV), X ∼B (n, p),
consider the ratio of the number X of successes in n Bernouli trials to the number n of trials.
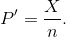 This new RV is called a proportion, and if the number of trials, n, is large
enough,
This new RV is called a proportion, and if the number of trials, n, is large
enough, 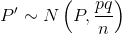 .
.
Q
Qualitative Data
See Data.
Quantitative Data
R
Relative Frequency
The ratio of the number of times a value of the data occurs in the set of all outcomes to the number of all outcomes.
S
Sample
A portion of the population understudy. A sample is representative if it characterizes the population being studied.
Standard Deviation
A number that is equal to the square root of the variance and measures how far data values are from their mean. Notation: s for sample standard deviation and σ for population standard deviation.
Standard Error of the Mean
The standard deviation of the distribution of the sample means, 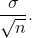 .
.
Standard Normal Distribution
A continuous random variable (RV) X-N (0, 1) .. When X follows the standard normal distribution, it is often noted as Z-N (0, 1).
Statistic
A numerical characteristic of the sample. A statistic estimates the corresponding population parameter. For example, the average number of full-time students in a 7:30 a.m. class for this term (statistic) is an estimate for the average number of full-time students in any class this term (parameter).
Student's-t Distribution
Investigated and reported by William S. Gossett in 1908 and published under the pseudonym Student. The major characteristics of the random variable (RV) are:
- It is continuous and assumes any real values.
- The pdf is symmetrical about its mean of zero. However, it is more spread out and fatter at the apex than the normal distribution.
- It approaches the standard normal distribution as n gets larger.
- There is a "family" of t distributions: every representative of the family is completely defined by the number of degrees of freedom which is one less than the number of data.
T
Type 1 Error
The decision is to reject the Null hypothesis when, in fact, the Null hypothesis is true.
U
Uniform Distribution
A continuous random variable (RV) that has equally likely outcomes over the domain, a < x < b. Often referred as the Rectangular distribution
because the graph of the pdf has the form of a rectangle. Notation: X~U (a, b). The mean is 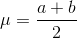 and the standard deviation is
and the standard deviation is 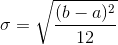 The probability density function is
The probability density function is 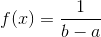 for
for 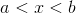 or
or 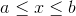 . The cumulative distribution is
. The cumulative distribution is 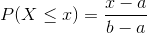 .
.
V
Variance
Mean of the squared deviations from the mean. Square of the standard deviation. For a set of data, a deviation can be represented as 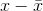 where x is a value of the data and
where x is a value of the data and 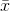 is the sample mean. The sample variance is equal to the sum of the squares of the
deviations divided by the difference of the sample size and 1.
is the sample mean. The sample variance is equal to the sum of the squares of the
deviations divided by the difference of the sample size and 1.
Z
z-score
The linear transformation of the form 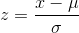 . If this
transformation is applied to any normal distribution X~N (µ, σ) , the result is the standard normal distribution Z~N (0, 1). If this transformation is applied to
any specific value x of the RV with mean µ and standard deviation σ , the result is called the z-score of x. Z-scores allow us to compare data that are
normally distributed but scaled differently.
. If this
transformation is applied to any normal distribution X~N (µ, σ) , the result is the standard normal distribution Z~N (0, 1). If this transformation is applied to
any specific value x of the RV with mean µ and standard deviation σ , the result is called the z-score of x. Z-scores allow us to compare data that are
normally distributed but scaled differently.
- 2478 reads






