In the graphs we have examined so far, adding a unit to the independent variable on the horizontal axis always has the same effect on the dependent variable on the vertical axis. When we add a passenger riding the ski bus, the ski club’s revenues always rise by the price of a ticket. The cancellation of one more game in the 1998–1999 basketball season would always reduce Shaquille O’Neal’s earnings by $210,000. The slopes of the curves describing the relationships we have been discussing were constant; the relationships were linear.
Many relationships in economics are nonlinear. A nonlinear relationship between two variables is one for which the slope of the curve showing the relationship changes as the value of one of the variables changes. A nonlinear curve is a curve whose slope changes as the value of one of the variables changes.
Consider an example. Suppose Felicia Alvarez, the owner of a bakery, has recorded the relationship between her firm’s daily output of bread and the number of bakers she employs. The relationship she has recorded is given in the table in Panel (a) of Figure 20.14. The corresponding points are plotted in Panel (b). Clearly, we cannot draw a straight line through these points. Instead, we shall have to draw a nonlinear curve like the one shown in Panel (c).
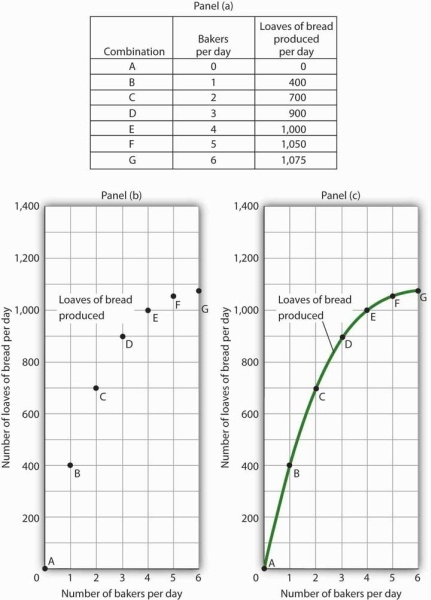
The table in Panel (a) shows the relationship between the number of bakers Felicia Alvarez employs per day and the number of loaves of bread produced per day. This information is plotted in Panel (b). This is a nonlinear relationship; the curve connecting these points in Panel (c) (Loaves of bread produced) has a changing slope.
Inspecting the curve for loaves of bread produced, we see that it is upward sloping, suggesting a positive relationship between the number of bakers and the output of bread. But we also see that the curve becomes flatter as we travel up and to the right along it; it is nonlinear and describes a nonlinear relationship.
How can we estimate the slope of a nonlinear curve? After all, the slope of such a curve changes as we travel along it. We can deal with this problem in two ways. One is to consider two points on the curve and to compute the slope between those two points. Another is to compute the slope of the curve at a single point.
When we compute the slope of a curve between two points, we are really computing the slope of a straight line drawn between those two points. In Figure 20.15, we have computed slopes between pairs of points A and B, C and D, and E and F on our curve for loaves of bread produced. These slopes equal 400 loaves/baker, 200 loaves/baker, and 50 loaves/baker, respectively. They are the slopes of the dashed-line segments shown. These dashed segments lie close to the curve, but they clearly are not on the curve. After all, the dashed segments are straight lines. Our curve relating the number of bakers to daily bread production is not a straight line; the relationship between the bakery’s daily output of bread and the number of bakers is nonlinear.
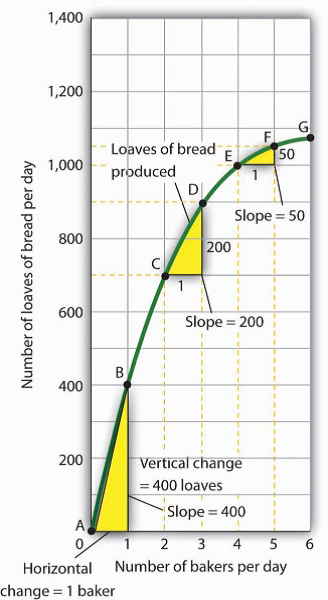
We can estimate the slope of a nonlinear curve between two points. Here, slopes are computed between points A and B, C and D, and E and F. When we compute the slope of a nonlinear curve between two points, we are computing the slope of a straight line between those two points. Here the lines whose slopes are computed are the dashed lines between the pairs of points.
Every point on a nonlinear curve has a different slope. To get a precise measure of the slope of such a curve, we need to consider its slope at a single point. To do that, we draw a line tangent to the curve at that point. A tangent line is a straight line that touches, but does not intersect, a nonlinear curve at only one point. The slope of a tangent line equals the slope of the curve at the point at which the tangent line touches the curve.
Consider point D in Panel (a) of Figure 20.16. We have drawn a tangent line that just touches the curve showing bread production at this point. It passes through points labeled M and N. The vertical change between these points equals 300 loaves of bread; the horizontal change equals two bakers. The slope of the tangent line equals 150 loaves of bread/baker (300 loaves/2 bakers). The slope of our bread production curve at point D equals the slope of the line tangent to the curve at this point. In Panel (b), we have sketched lines tangent to the curve for loaves of bread produced at points B, D, and F. Notice that these tangent lines get successively flatter, suggesting again that the slope of the curve is falling as we travel up and to the right along it.
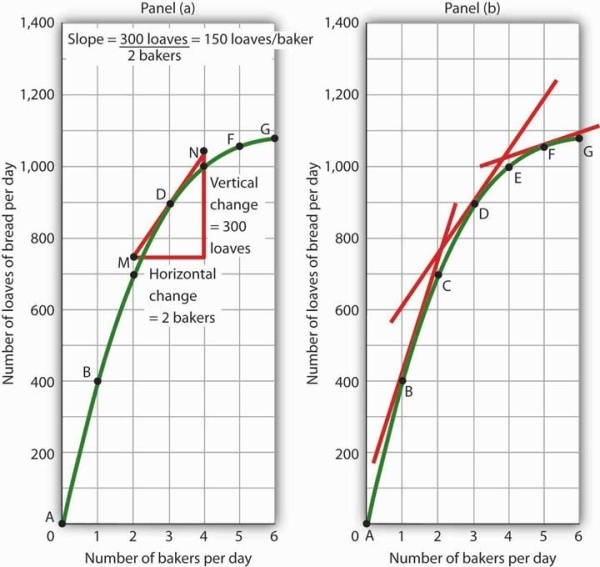
Because the slope of a nonlinear curve is different at every point on the curve, the precise way to compute slope is to draw a tangent line; the slope of the tangent line equals the slope of the curve at the point the tangent line touches the curve. In Panel (a), the slope of the tangent line is computed for us: it equals 150 loaves/baker. Generally, we will not have the information to compute slopes of tangent lines. We will use them as in Panel (b), to observe what happens to the slope of a nonlinear curve as we travel along it. We see here that the slope falls (the tangent lines become flatter) as the number of bakers rises.
Notice that we have not been given the information we need to compute the slopes of the tangent lines that touch the curve for loaves of bread produced at points B and F. In this text, we will not have occasion to compute the slopes of tangent lines. Either they will be given or we will use them as we did here—to see what is happening to the slopes of nonlinear curves.
In the case of our curve for loaves of bread produced, the fact that the slope of the curve falls as we increase the number of bakers suggests a phenomenon that plays a central role in both microeconomic and macroeconomic analysis. As we add workers (in this case bakers), output (in this case loaves of bread) rises, but by smaller and smaller amounts. Another way to describe the relationship between the number of workers and the quantity of bread produced is to say that as the number of workers increases, the output increases at a decreasing rate. In Panel (b) of Figure 20.16 we express this idea with a graph, and we can gain this understanding by looking at the tangent lines, even though we do not have specific numbers. Indeed, much of our work with graphs will not require numbers at all.
We turn next to look at how we can use graphs to express ideas even when we do not have specific numbers.
- 瀏覽次數:3015






