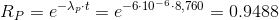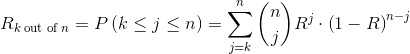If two components arranged in parallel are similar and have constant failure rate λ, the reliability of the system RP can be calculated with Table 4.4 , wherein RC is the reliability of the component RC=e−λt:
|
|
The calculation of the MTTF leads to 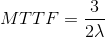 . In
fact we have:
. In
fact we have:
|
|
Therefore, the MTTF increases compared to the single component CFR. The failure rate of the parallel system λP, reciprocal of the MTTF, is:
|
|
As you can see, the failure rate is not halved, but was reduced by one third.
For example, let us consider a safety system which consists of two batteries and each one is able to compensate for the lack of electric power of the grid. The two generators are equal and have a constant failure rate λB=9∙10−6 failures per hour. We’d like to calculate the failure rate of the system, the MTTF and reliability after one year of continuous operation.
As in the previous case, we start with a reliability block diagram of the problem, as visible in Figure 4.15 .
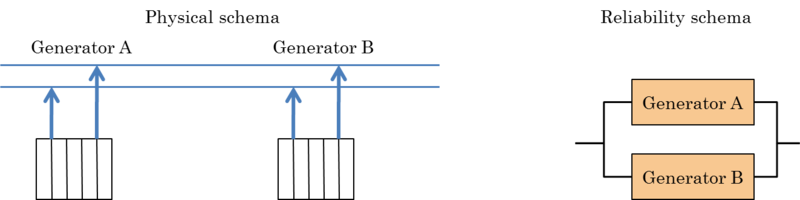
It is a parallel arrangement, for which the following equation is applicable:
|
|
The MTTF is the reciprocal of the failure rate and is:
|
|
As a year of continuous operation is 24⋅365=8,760 hours, the reliability after one year is:
|
|
It is interesting to calculate the reliability of a system of identical elements arranged in a parallel configuration k out of n. The system is partially redundant since a group of k elements is able to withstand the load of the system. The reliability is:
|
|
Let us consider, for example, three electric generators, arranged in parallel and with failure rate λ=9⋅10−6. In order for the system to be active, it is sufficient that only two items are in operation. Let’s get the reliability after one year of operation.
We’ll have: n=3, k=2. So, after a year of operation (t=8760 h), reliability can be calculated as follows:
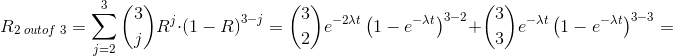
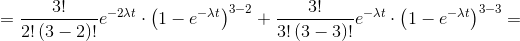
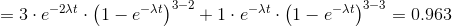
A particular arrangement of components is that of the so-called parallel with stand-by: the second component comes into operation only when the first fails. Otherwise, it is idle.
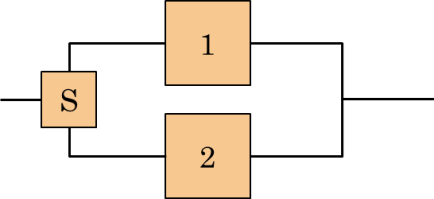
If the components are similar, then λ1=λ2. It’s possible to demonstrate that for the stand-by parallel system we have:
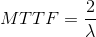
|
Thus, in parallel with stand-by, the MTTF is doubled.=
- 3424 reads





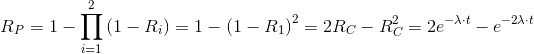
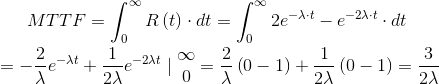
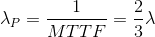
![\lambda _{P}=\frac{2}{3}\lambda =\frac{2}{3}9\cdot 10^{-6}= 6\cdot 10^{-6}\left [\frac{\textrm{guasti}}{\textrm{h}}\right ]](/system/files/resource/18/18769/18979/media/eqn-img_4.gif)
![MTTF=\frac{1}{\lambda _{P}}= \frac{1}{6\cdot 10^{-6}}=166,666\left [ \textrm{h} \right ]](/system/files/resource/18/18769/18979/media/eqn-img_5.gif)