Shift Registers allow the preservation of intermediate results between sequences of iterations.
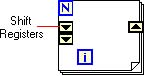
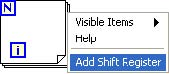
To add a Shift Register, right click on the For Loop structure and select Add Shift Register from the pop-up menu.
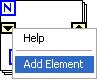
To add elements to the shift register, right click on the shift register and select Add Element from the pop-up menu.
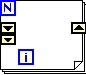
To illustrate the use of the shift registers, the following example computes the Fibonacci number Fib(n).
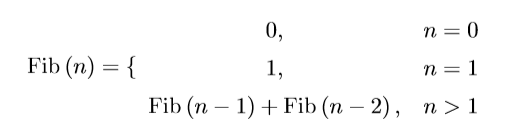
In the Front Panel window, select an integer 32 numeric input and output controls and labeled them n and Fib(n) respectively. Arrange the diagram as shown in Shift Register Example.
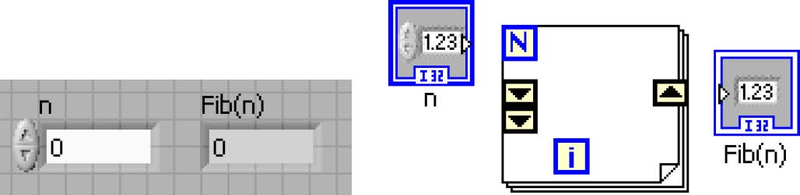
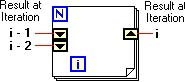
Add a 0 and 1 numeric constants to initialize the elements of the shift register and wire them to the i-1 and i-2 elements respectively. Add the add operator in the for loop and complete the program wiring as shown in Fibonacci G Program.
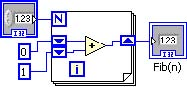
For n=0, the for loop iterates 0 times and passes 0 to Fib(n), therefore Fib(0) 0. For n 1, the for loop the values ini-1 and i-2 shift register elements are added (0+1) and saved in the i shift register element (1). Since the loop iterates once only, the resulting value is passed toFib(n), therefore Fib(1) 1. For n= 2, the first iteration produces the value of 1. Prior to the next and final iteration, the values are shifted in the register as follows:
The value in the i-2 shift register element is discarded
The value in the i-1 shift register element is shifted to the i-2 shift register element
The value in the i shift register element is shifted to thei-1 shift register element
To start the 2nd and final iteration, thei-1 shift register element contains 1 and the i-2 shift register element contains 0. These are added to produce 1, which is passed to Fib(n) and, therefore, Fib(2) 1. This process is repeated for values of n > 2.
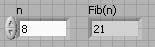
Save this program as Fibonacci.vi. Figure 7.29 shows the result of Fib(8).
- 2000 reads






