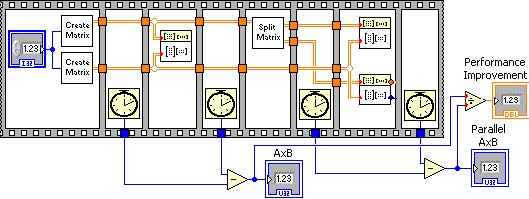
Matrix multiplication is a compute intensive operation that can leverage data parallelism. Figure Data Parallelism shows a G program with 8 sequential frames to demonstrate the performance improvement via data parallelism.
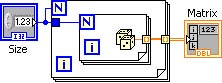
The Create Matrix function generates a square matrix based of size indicated by Size containing random numbers between 0 and 1. The Create Matrix function is shown in Figure Creating a Square Matrix.
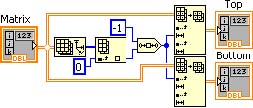
The Split Matrix function determines the number of rows in the matrix and shifts right the resulting number of rows by one (integer divide by 2). This value is used to split the input matrix into the top half and bottom half matrices. The Split Matrix function is shown in Figure Split Matrix into Top & Bottom.
| Sequence Frame | Operation Description |
| First Frame | Generates two square matrices initialized with random numbers |
| Second Frame | Records start time for single core matrix multiply |
| Thrid Frame | Performs single core matrix multiply |
| Fourth Frame | Records stop time of single core matrix multiply |
| Fifth Frame | Splits the matrix into top and bottom matrices |
| Sixth Frame | Records start time for multicore matrix multiply |
| Seventh Frame | Performs multicore matrix multiply |
| Eighth Frame | Records stop time of multicore matrix multiply |
The rest of the calculations determine the execution time in milliseconds of the single core and multi-core matrix multiply operations and the performance improvement of using data parallelism in a multicore computer.
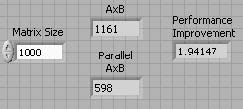
The program was executed in a dual core 1.83 GHz laptop. The results are shown in Figure Data Parallelism Performance Improvement. By leveraging data parallelism, the same operation has nearly a 2x performance improvement. Similar performance benefts can be obtained with higher multicore processors
- 2195 reads






