在前面的部分中,我们介绍了诸如总体参数、样本统计量、样本偏差等术语。在本部分,我们将试图了解这些术语的意思以及它们如何相互关联。
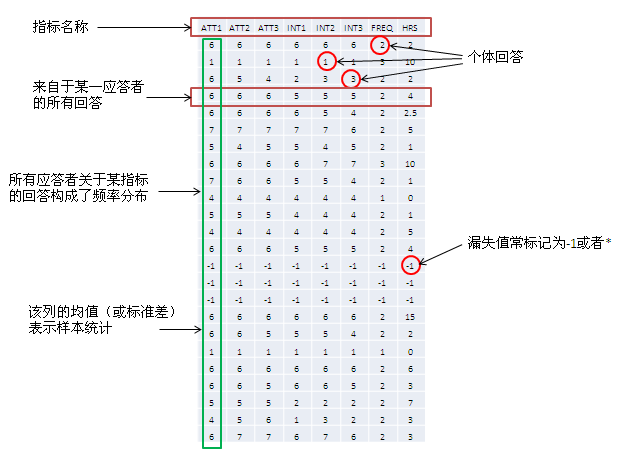
当测量一个给定的分析单元的某个观察时,比如一个人对李克特式量表项目的回应,那个观察就叫做回应(见图表 8.2)。换句话说,回应是一个单元样本提供的测量值。每个受访者对一张表上的不同的项目有不同的回应。可以根据不同受访者对相同项目或观测的回应发生的频率绘制频率分布图。对于样本中的大多数回应,这个频率分布趋向于一个钟形曲线,称作正态分布,它可以用来估计全部样本的特性,如样本均值(样本中所有观测的平均数)或标准误(样本中所有观察的变异性或差幅)。这些样本估计称作样本统计量(“统计量”是一个值,这个值就是观测数据的估计)。如果能够对全部总体取样,也将获得总体的均值和标准误。然而,总体不能全部取样,总体特征总是未知的,它们称作总体参数(而不是“统计量”,因为它们不能通过数据的统计分析得到估计)。如果样本不能完美地代表总体,样本统计量可能与总体参数不同。两者间的差异称作抽样误差。从理论上讲,如果我们可以逐渐增加样本容量,样本越来越接近总体数量,那么抽样误差将会降低,样本统计量将与相应的总体参数越来越近似。
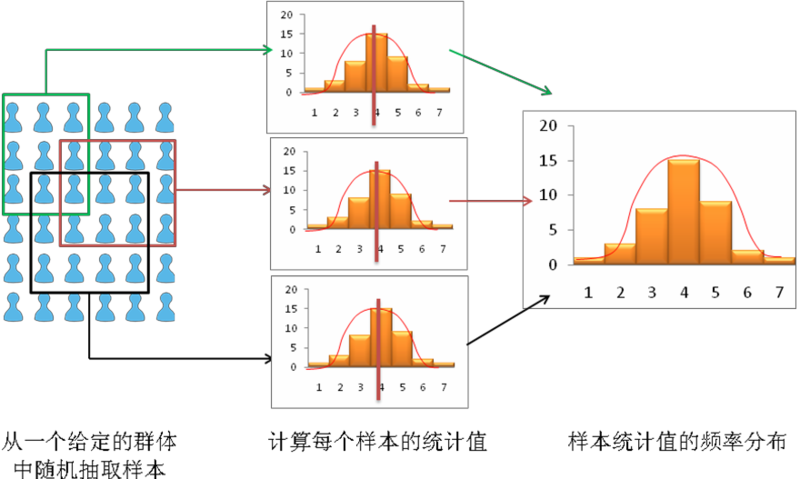
如果一个样本真正代表了总体,那么估计的样本统计量应该与相应的理论总体参数完全相同。我们怎么才能知道样本统计量是否至少合理地接近总体参数?在这里我们需要了解抽样分布的概念。假设从给定的总体中选取三个不同的随机样本,如图表 8.3所示,并推断出每个样本的样本均值和标准误等样本统计量。如果每个样本都真正代表了总体,那么三个随机样本的三个样本均值将是相等的(并且与总体参数相等),样本均值的标准差将是零。但是这是极不可能的,因为每个随机样本可能由总体的不同子集构成,因此,它们的均值可能会有微小的不同。然而,可以取这三个均值绘制样本均值的频率直方图。如果这些样本的数量从10增加到100,频率直方图成为抽样分布。因此,一个抽样分布是一系列样本的样本统计量的频率分布,而作为参考的一般频率分布是单个样本的回应(观测)的分布。就像一个频率分布,抽样分布也往往有更多聚集在均值(当然是总体参数的估计)周围的样本统计量。无限大的样本的分布将接近正态分布。抽样分布的样本统计量的变异性或差幅(即,抽样统计量的标准差)称作标准误。相比之下,标准差这个术语用于单个样本观测值的变异性。
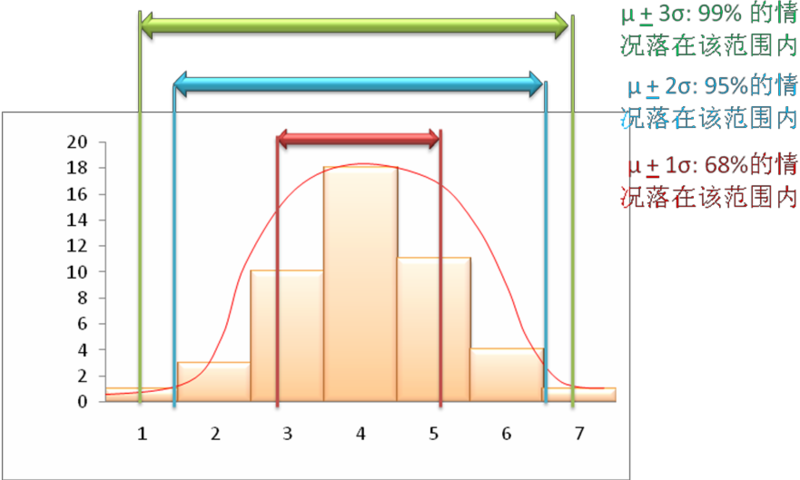
所在抽样分布中抽样统计量的均值被认为是未知总体参数的估计。基于抽样分布的差幅(即,基于标准误),也可以估计总体参数预测的置信区间。置信区间是总体参数落于某个特定样本统计值区间的概率。有的正态分布倾向于遵循68-95-99百分比法则(见图表 8.4),它表示在这个分布中超过68%的样本分布在均值的一个标准偏差范围之内(μ+1σ),超过95%的样本分布在均值的两个标准偏差范围之内(µ+2σ),以及超过99%的样本分布在均值的三个标准偏差范围之内(µ+3σ)。
因为有无限样本数的抽样分布接近正态分布,68-95-99法则也同样适用于抽样分布,可以这样表述:
(样本统计+标准误)代表了总体参数68%的置信区间。
(抽样统计+两个标准误)代表了总体参数95%的置信区间。
(抽样统计+三种标准误)代表了总体参数99%的置信区间。
如果抽样分布无法估计或违反了68-95-99百分比法则,样本就是有偏的(不能代表总体)。另外值得注意的是,在大多数用p<0.05检验系数显著性的回归分析中,我们正试图看看抽样统计(回归系数)是否在95%的置信区间预测了相应总体参数(真实数值)。有趣的是,“六个δ”标准尝试识别99%的置信区间以外的或是六个标准差(用希腊字母δ表示),代表p<0.01时的显著性检测。
- 6604 reads






