最简单的推理分析之一就是比较事后测试的实验组和对照组的结果,比如进入一项特别数学项目的学生是否比那些传统数学课程的学生表现得更好。在这个例子中,预测变量是一个虚拟变量(1=实验组,0=对照组),同时结果变量,即表现,是一个定比变量(比如,在特别项目之后的一个数学测试的分数)。这个简单设计的分析技术是单因素方差分析(单因素是因为它只包含了一个预测变量),统计检验被称为学生(Student)t检验(或者简略地成为t检验)。
t检验于1908年被一个在爱尔兰都柏林的吉尼斯啤酒厂工作的化学家威廉·西利·戈塞特用于控制烈性黑啤酒的质量,这种黑啤酒在19世纪伦敦的守门人中很受欢迎。因为他的雇主不想暴露他们使用了统计方法来控制质量的事实,戈塞特在《生物统计学》上使用自己的笔名“学生”发表了这个检验方法(他曾经是罗纳德·费舍尔爵士的学生),同时这个检验需要计算t值,t这个字母经常被费舍尔用来表示两组之间的差异。因此,这个检验被称为学生t检验,虽然这个学生的身份对于统计学家而言都是熟知的。
t检验研究两组的均值是否在统计上有差别(非定向或双尾检验),或者一组的均值在统计上比另外一组要大(或小)(定向或者单尾检验)。在我们的例子中,如果我们想检验在特殊数学课程中学习的学生是否比那些在传统课程中学习的学生表现更好,我们需要一个单尾检验。这个假设可以这样写:
H0:μ1≤μ2 (原假设)
H1:μ1>μ2 (被择假设)
μ1表示参加了特别课程的学生的表现的均值(实验组),μ2表示参加了传统课程的学生的表现的均值(对照组)。注意,原假设永远是有等于号的那一个,所有的统计显著性检验都是为了拒绝原假设。
我们怎样能够用从不同总体中抽取的样本来推测出总体均值的差别呢?从图表
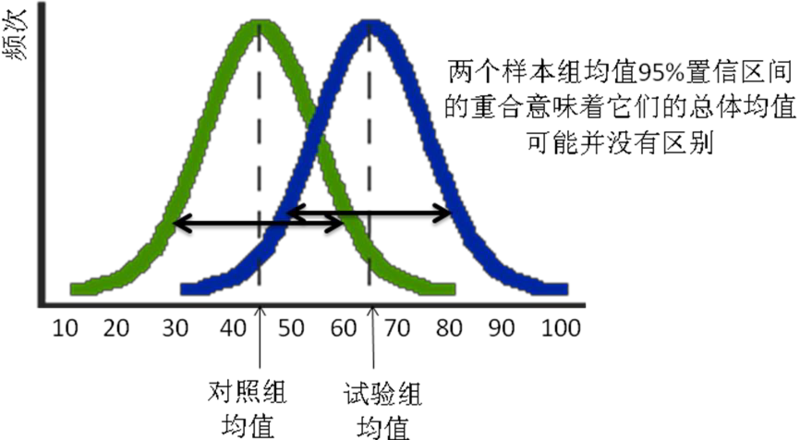
15.2中的假设的实验组和对照组分数的频数分布中我们可以看到,对照组似乎有一个平均分数为45(在0-100的区间上)的钟形(正态)分布,而实验组看起来平均分数为65。这两个均值看起来是有差异的,但是他们实际上是样本的均值(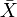 ),由于抽样误差的存在,这可能与它们所对应的总体均值(μ)有差异。样本均值是在一定置信区间对总体参数的概率估计(95%的置信区间是样本均值+两个标准误差,其中标准误是从总体中抽取出的无限个样本的均值的分布的标准差)。因此,总体均值的统计显著性不仅仅依赖于样本均值的数值,也依赖于标准误或者说样本均值频数分布的发散度。如果发散度很大(比如,这两条钟形曲线有很多重叠),那么这两个均值的95%的置信区间也可能会重叠,这样我们就不能得出高可能性的(p<0.05)他们相对应的总体均值显著不同的结论。然而,如果这两条曲线的发散度较低(即,他们重叠的部分很少),那么每个均值的置信区间就可能不会重叠,这样我们就可以拒绝原假设,认为这两个总体均值在p<0.05的水平下显著不同。
),由于抽样误差的存在,这可能与它们所对应的总体均值(μ)有差异。样本均值是在一定置信区间对总体参数的概率估计(95%的置信区间是样本均值+两个标准误差,其中标准误是从总体中抽取出的无限个样本的均值的分布的标准差)。因此,总体均值的统计显著性不仅仅依赖于样本均值的数值,也依赖于标准误或者说样本均值频数分布的发散度。如果发散度很大(比如,这两条钟形曲线有很多重叠),那么这两个均值的95%的置信区间也可能会重叠,这样我们就不能得出高可能性的(p<0.05)他们相对应的总体均值显著不同的结论。然而,如果这两条曲线的发散度较低(即,他们重叠的部分很少),那么每个均值的置信区间就可能不会重叠,这样我们就可以拒绝原假设,认为这两个总体均值在p<0.05的水平下显著不同。
为了进行t检验,我们必须首先计算一个t统计量,表示这两组样本均值的差别。这个统计量是两个样本均值的差与它们的分数之差的变异程度(标准误)的比值:
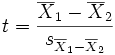
其中分子是实验组(组1)和对照组(组2)的样本均值之间的差异,分母是这两组之间差异的标准误,分母也可以这样来估计:
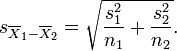
s2是方差,n是每一组的样本规模。如果实验组的均值比对照组的均值大,t统计量会为正。为了确定t统计量是否足够大而不是偶然地为正,我们必须从标准统计课本中的统计表中或者因特网上查阅与我们计算出的t统计量相关的概率或p值,或者使用统计软件程序比如SAS和SPSS来计算。这个值是一个关于t统计量,t检验是单尾还是双尾,和自由度(df)或者在计算这个统计量时能够自由变动的值的数量的函数(通常是一个样本容量和所进行的检验的类型的函数)。t检验的自由度的计算方法如下:
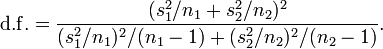
通常接近于(n1+n2–2)。如果p值比理想的显著性水平(例如α=0.05),或者得出有实验处理效应而实质上没有(I类错误)的结论时我们愿意承担的最大风险(可能性)要小,我们就可以拒绝原假设。
在研究了实验组是否显著地比对照组有更高的均值之后,通常来说,下一个问题是效应规模或者是相对于对照组的试验处理效应的大小是多少?我们可以通过进行一个代表表现分数的结果变量(y)与一个代表是否是实验组的虚拟预测变量(x)的双变量一般线性回归来进行回归分析。实验变量的回归系数(β1)同时也是回归线的斜率(β1=Δy/Δx),就是对效应规模的预测值。在上面的例子中,由于x是一个只有两个值(0和1)的虚拟变量,因此效应规模或者β1就是实验组和对照组均值的差异(Δy=y1-y2)。
- 8802 reads






