社会科学研究中的大部分推断统计程序都来源于一组统计模型,叫做一般线性模型(general linear model,GLM)。一个模型是指一个估计的数学方程,它可以用来代表一组数据,而线性是指一条直线。因此,一个GLM是指可以用来代表观察数据中的一种线性关系的一个方程组。
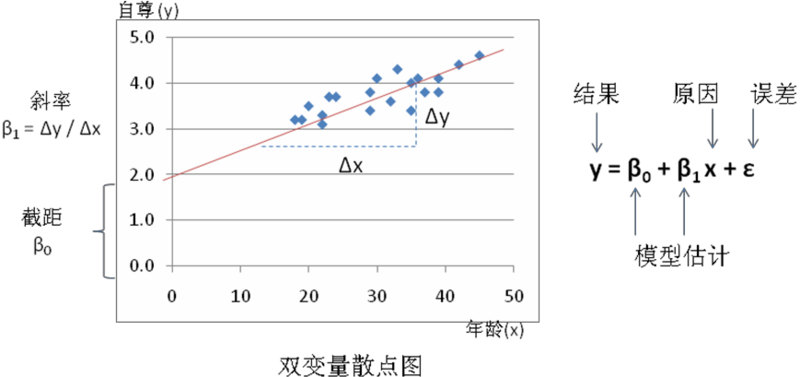
最简单的GLM是研究自变量(原因或者预测因素)与因变量(影响或者结果)之间关系的双变量线性模型。我们假设这两个变量分别是年龄和自尊,二者关系的二元散点图见图表 15.1,水平线或者X轴表示年龄(预测因素),垂直线或者Y轴表示自尊(结果)。散点图
显示,代表同时被标注出年龄和自尊的个体观测者的点在图中沿着一条虚构的向上倾斜的直线分布。我们可以通过GLM估计这条线的参数,比如它的斜率和截距。从高中的代数中我们知道,这条线可以用数学方程y=mx+c来代表,其中m是这条直线的斜率(x每变动一个单位,y变动的值),c是截距项(当x等于0的时候,y的值)。在GLM中,这个方程正式地表示为:
y=β0+β1x+ε
其中β0是斜率,β1是截距项,ε是误差项。由于大部分观测值都很接近那条线但并不是刚刚落到那条线上(即GLM不是完美的),所以存在ε来表示实际观察值与它们的估计值之间的偏差。注意一个线性模型可以有两个以上的预测因素。为了形象地表示一个有两个预测因素的线性模型。我们一个想象一个三维的立方体,结果(y)用垂直轴表示,两个预测因素(比如,x1和x2)用立方体的两条水平轴表示。一条描述两个或者更多变量之间关系的线叫做回归线,β0和β1(以及其他的贝塔值)都被称为回归系数,而估计回归系数的过程被叫做回归分析。有n个预测因素的回归分析GLM见下:
y=β0+β1x1+β2x2+β3x3+…+βnxn+ε
在上面的方程中,预测变量xi可以代表自变量或者协变量(控制变量)。协变量是我们在理论上不感兴趣的变量,但是它们可能会对因变量y有影响,所以应该被控制,这样我们感兴趣的自变量的残余影响能够被更加精确地检测出来。协变量抓住了一个回归方程中的系统误差,而误差项(ε)则抓住了随机误差。虽然GLM中的大部分变量往往是等距或者等比变量,但也不必要总是这样。一些预测变量甚至可以是名义变量(例如,性别:男性或女性),他们被编码为虚拟变量。这些变量假定只能从两个可能的值当中取其中之一,这两个可能的值为0或1(在性别的例子中,“男性”被指定为0,“女性”被指定为1;反之亦然)。n个定类变量用n-1个虚拟变量来表示。比如,包括农业、制造业和服务业的产业类别,可以用两个联合的虚拟变量(x1,x2)来表示,(0,0)代表农业,(0,1)代表制造业,(1,1)代表服务业。我们不用关心赋予不用的类别多大的值,是0还是1,因为0和1被认为是两个截然不同的组,而不是数字量(就像在一个实验设计中的实验组和对照组一样),而每一个组的统计参数都是分别估计的。
GLM是一个非常强有力的统计工具,因为它不是一个单一的统计方法,而是一组可以被用来分析不同种类和大量预测变量与结果变量之间复杂关系的方法。如果我们有一个虚拟预测变量,同时我们在比较这个变量的两个取值(0和1)对结果变量的影响,那么我们在进行一个方差分析。如果我们在控制了一个或者多个协变量之后进行方差分析,那么我们在进行一个协方差分析。我们也可以有多个结果变量(比如,y1,y1,…yn),可以用一个方程组来表示,对于方程组中的每个结果变量都对应着一个不同的方程(每个方程都有自己的回归系数)。如果多个结果变量都被同一组预测变量来解释,这种分析被称为多变量回归。如果我们使用多个结果变量来进行方差分析或者协方差分析,这种分析被称为多变量方差分析或者是多变量协方差分析。如果我们在一个相关联的方程组中使用一个回归方程的结果作为另外一个回归方程的预测因素,那么我们就得到一个非常复杂的类型的分析,被称为结构方程模型。在GLM中最为重要的问题就是模型设定,即怎么确定一个回归方程(或一个方程组)来最好地描述我们所关心的现象。模型设定应该基于对所研究的现象的理论思考,而不是什么模型能够最好地拟合观测数据。数据是用来验证模型的,而不是用来设定模型的。
- 8859 reads






