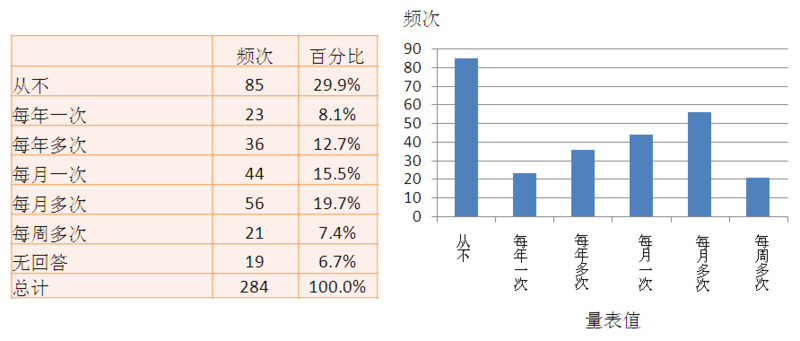
一元分析,或单变量分析,是指可以描述一个变量总体属性的一套统计方法。单变量统计包括:(1)频数分布,(2)集中趋势,和(3)离差。一个变量的频数分布是那个变量的单个值或是范围值的频数(或百分比)。例如,我们可以度量一个样本的调查对象参加了多少次宗教服务(表示他们的“宗教性”的一个变量),通过用一个分类尺度:从来不,每年一次,每年几次,大约每月一次,每月几次,一周几次,和一个对于“不回答”的选择性分类。如果我们计数每个分类(除了“不回答”,实际表示一个缺失值而不是一个分类)下的观测值数量(或百分比),并以表格的形式列示,如图表 14.1。这就是频数分布。这个分布也可以以直方图的形式描绘出,即图表 14.1右侧,横轴表示那个变量的每个分类,纵轴表示每类中观测值的频数或百分比。
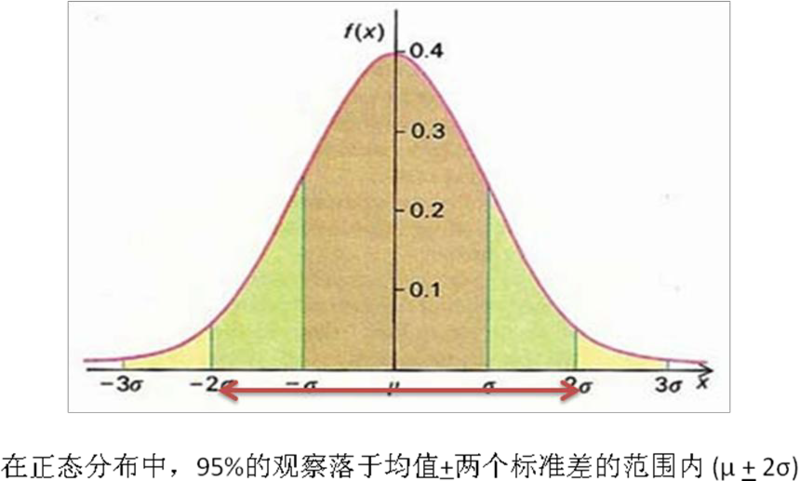
由于许多大样本的观测值是独立和随机的,频数分布倾向于逼近一个图,看起来像钟形曲线(频数分布的一个光滑的直方图),类似于图表 14.2所示,大多数观测值向中心聚集,越来越少的观测值趋向极端。这样的曲线叫正态分布。
集中趋势是分布的中心值的估计。有三种集中趋势的主要估计:均值、中位数和众数。算术平均值(经常仅被叫做“均值”)是一个给定分布的所有值的简单平均。考虑一组8测试得分:15,22,21,18,36,15,25,15.这些值的算术平均数是(15+20+21+20+36+15+25+15)/8=20.875.其他类型的均值包括几何平均数(一个n个数值分布的n次方根)和协和平均数(一个分布中每个值的倒数的算术平均数的倒数),但是这些均值在社会研究数据的统计分析中不是很流行。
第二种计量集中趋势的方法——中位数,是一个分布的值域的中间值。这通过用增序排列所有的值并挑出中间值计算得到。在有两个中间值的情况下(如果分布有偶数个值),这个两个中间值的平均数代表中位数。在上述例子中,排序后的值是:15,15,15,18,22,21,25,36.这两个中间值是18和22,因此中位数是(18+22)/2=20.
最后,众数是值的分布中出现最频繁的值。在前述例子中,最频繁出现的值是15,这就是上述测试得分的众数。注意从样本中估计出的任何值,比如均值、中位数、众数,或者任何后来的估计都叫统计。
离差是指值分布于集中趋势周围的方式,例如,值是怎样紧密或怎样广泛聚集在均值周围的。两种普遍的离差的测度是极差和标准差。极差是最高值和最低值之间的差异。我们前述例子中极差是36-15=21.
极差对极端值的出现特别敏感。例如,如果上述分布的最高值是85,其他值保持不变,极差就是85-15=70。标准差,第二种离差的测度,通过使用一个公式修正了这种极端值。这个公式考虑了每个变量与分布的均值的距离:
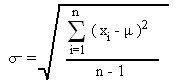
σ是标准差,xi是第i个观测(或值),µ是算术平均数,n是观测值的数量,Σ表示所有观测值的总和。标准差的平方叫做分布的方差。在正态的频数分布中,68%的观测值位于均值的一倍标准差之间(µ+1σ),95%的观测值在两倍标准差之间(µ+2σ),99.7%的观测值位于三倍标准差内(µ+3σ),如图表 14.2所示。
- 6543 reads






