Musical tones are produced by musical instruments, or by the voice, which, from a physics perspective, is a very complex wind instrument. So the physics of music is the physics of the kinds of sounds these instruments can make. What kinds of sounds are these? They are tones caused by standing waves produced in or on the instrument. So the properties of these standing waves, which are always produced in very specific groups, or series, have far-reaching effects on music theory.
Most sound waves, including the musical sounds that actually reach our ears, are not standing waves. Normally, when something makes a wave, the wave travels outward, gradually spreading out and losing strength, like the waves moving away from a pebble dropped into a pond.
But when the wave encounters something, it can bounce (reflection) or be bent (refraction). In fact, you can "trap" waves by making them bounce back and forth between two or more surfaces.
Musical instruments take advantage of this; they produce pitches by trapping sound waves.
Why are trapped waves useful for music? Any bunch of sound waves will produce some sort of noise. But to be a tone - a sound with a particular pitch - a group of sound waves has to be very regular, all exactly the same distance apart. That's why we can talk about the frequency (pg 99) and wavelength (pg 99) of tones.
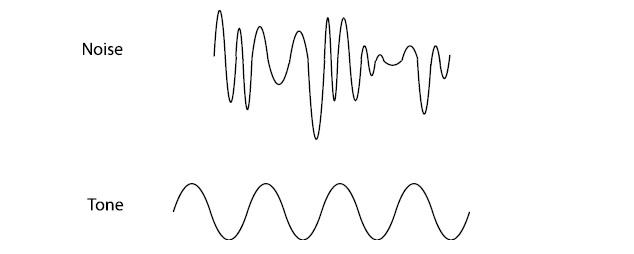
So how can you produce a tone? Let's say you have a sound wave trap (for now, don't worry about what it looks like), and you keep sending more sound waves into it. Picture a lot of pebbles being dropped into a very small pool. As the waves start reffecting off the edges of the pond, they interfere with the new waves, making a jumble of waves that partly cancel each other out and mostly just roils the pond - noise.
But what if you could arrange the waves so that reffecting waves, instead of cancelling out the new waves, would reinforce them? The high parts of the reffected waves would meet the high parts of the oncoming waves and make them even higher. The low parts of the reffected waves would meet the low parts of the oncoming waves and make them even lower. Instead of a roiled mess of waves cancelling each other out, you would have a pond of perfectly ordered waves, with high points and low points appearing regularly at the same spots again and again. To help you imagine this, here are animations of a single wave reffecting back and forth8 and standing waves.
This sort of orderliness is actually hard to get from water waves, but relatively easy to get in sound waves, so that several completely different types of sound wave "containers" have been developed into musical instruments. The two most common - strings and hollow tubes - will be discussed below, but first let's finish discussing what makes a good standing wave container, and how this affects music theory.
In order to get the necessary constant reinforcement, the container has to be the perfect size (length) for a certain wavelength, so that waves bouncing back or being produced at each end reinforce each other, instead of interfering with each other and cancelling each other out. And it really helps to keep the container very narrow, so that you don't have to worry about waves bouncing off the sides and complicating things. So you have a bunch of regularly-spaced waves that are trapped, bouncing back and forth in a container that fits their wavelength perfectly. If you could watch these waves, it would not even look as if they are traveling back and forth. Instead, waves would seem to be appearing and disappearing regularly at exactly the same spots, so these trapped waves are called standing waves.
For any narrow "container" of a particular length, there are plenty of possible standing waves that don't fit. But there are also many standing waves that do fit. The longest wave that fits it is called the fundamental. It is also called the first harmonic. The next longest wave that fits is the second harmonic, or the first overtone. The next longest wave is the third harmonic or second overtone, and so on.
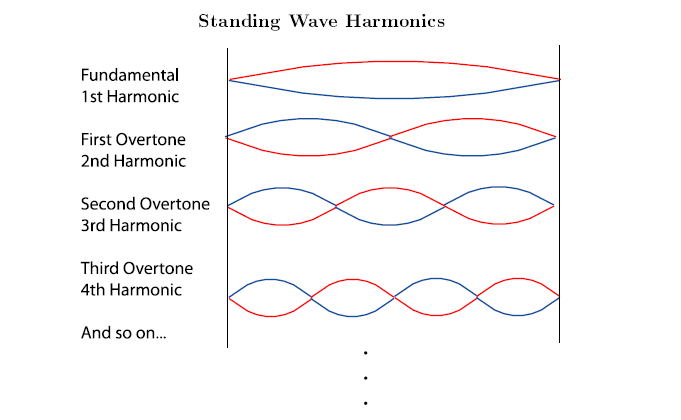
Notice that it doesn't matter what the length of the fundamental is; the waves in the second harmonic must be half the length of the first harmonic; that's the only way they'll both "fit". The waves of the third harmonic must be a third the length of the first harmonic, and so on. This has a direct effect on the frequency and pitch of harmonics, and so it affects the basics of music tremendously. To find out more about these subjects, please see Frequency, Wavelength, and Pitch10, Harmonic Series, or Musical Intervals, Frequency, and Ratio.
- 2820 reads






