In a way, equal temperament is a compromise between the Pythagorean approach and the meantone approach. Neither the third nor the fifth is pure, but neither of them is terribly far off, either. Because equal temperament divides the octave into twelve equal semi-tones (half steps), the frequency ratio of each semi-tone is the twelfth root of 2. If you do not understand why it is the twelfth root of 2 rather than, say, one twelfth, please see the explanation below. (There is a review of powers and roots in Powers, Roots, and Equal Temperament16 if you need it.)

In equal temperament, the only pure interval is the octave. (The twelfth power of the twelfth root of two is simply two.) All other intervals are given by irrational numbers based on the twelfth root of two, not nice numbers that can be written as a ratio of two small whole numbers. In spite of this, equal temperament works fairly well, because most of the intervals it gives actually fall quite close to the pure intervals. To see that this is so, look at Figure 6.5. Equal temperament and pure intervals are calculated as decimals and compared to each other. (You can find these decimals for yourself using a calculator.)
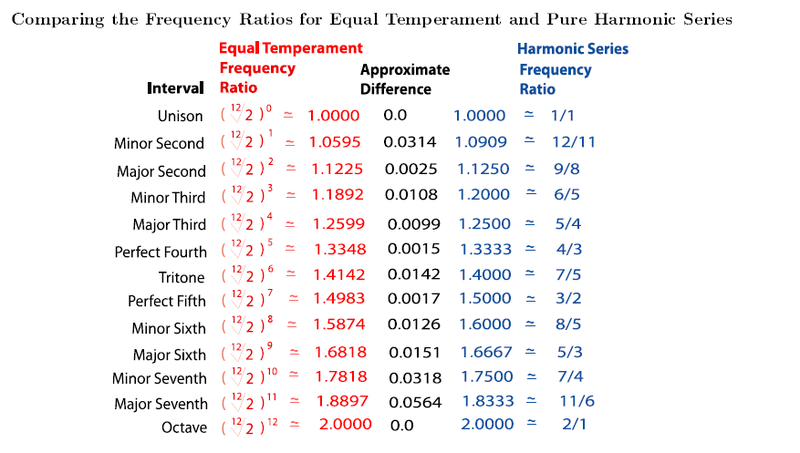
Except for the unison and the octave, none of the ratios for equal temperament are exactly the same as for the pure interval. Many of them are reasonably close, though. In particular, perfect fourths and fifths and major thirds are not too far from the pure intervals. The intervals that are the furthest from the pure intervals are the major seventh, minor seventh, and minor second (intervals that are considered Consonance and Dissonance anyway).
Because equal temperament is now so widely accepted as standard tuning, musicians do not usually even speak of intervals in terms of ratios. Instead, tuning itself is now defined in terms of equal-temperament, with tunings and intervals measured in cents. A cent is 1/100 (the hundredth root) of an equal-temperament semitone. In this system, for example, the major whole tone discussed above measures 204 cents, the minor whole tone 182 cents, and a pure fifth is 702 cents.
Why is a cent the hundredth root of a semitone, and why is a semitone the twelfth root of an octave? If it bothers you that the ratios in equal temperament are roots, remember the pure octaves and fifths of the harmonic series.

Every octave has the same frequency ratio; the higher note will have 2 times the frequency of the lower note. So if you go up another octave from there (another 2 times), that note must have 2 x 2, or 4 times the frequency of the lowest note. The next octave takes you up 2 times higher than that, or 8 times the frequency of the first note, and so on.
In just the same way, in every perfect fifth, the higher note will have a frequency one and a half (3/2) times the lower note. So to find out how much higher the frequency is after a series of perfect fifths, you would have to multiply (not add) by one and a half (3/2) every time you went up another perfect fifth.
All intervals work in this same way. So, in order for twelve semitones (half steps) to equal one octave, the size of a half step has to be a number that gives the answer "2" (the size of an octave) when you multiply it twelve times: in other words, the twelfth root of two. And in order for a hundred cents to equal one semitone, the size of a cent must be the number that, when you multiply it 100 times, ends up being the same size as a semitone; in other words, the hundredth root of the twelfth root of two. This is why most musicians prefer to talk in terms of cents and intervals instead of frequencies.
- 16138 reads






