Solution to Exercise 4.1:

Solution to Exercise 4.2:
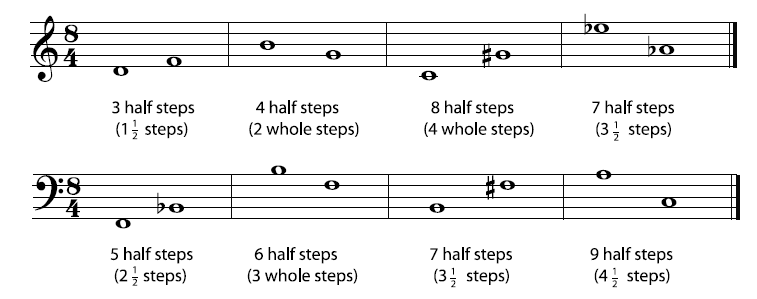
Solution to Exercise 4.3:

Solution to Exercise 4.4:
- Major
- Major
- Minor
- Major
- Minor
Solution to Exercise 4.5:

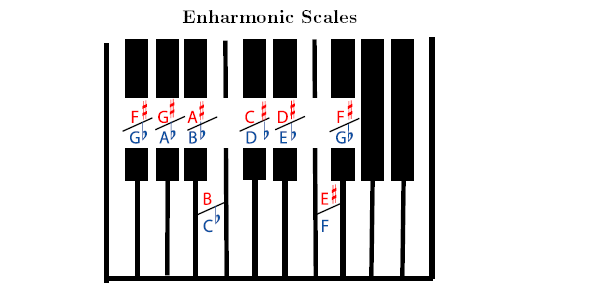
Notice that although they look completely different, the scales of F sharp major and G flat major (numbers 5 and 6) sound exactly the same when played, on a piano as shown in the following Figure 4.59, or on any other instrument using equal temperament tuning. If this surprises you, please read more about enharmonic scales.
Solution to Exercise 4.6:

Solution to Exercise 4.7:
- A minor: C major
- G minor: B flat major
- B flat minor: D flat major
- E minor: G major
- F minor: A flat major
- F sharp minor: A major
Solution to Exercise 4.8:

Solution to Exercise 4.9:

Solution to Exercise 4.10:

Solution to Exercise 4.11:

Solution to Exercise 4.12:

Solution to Exercise 4.13:

Solution to Exercise 4.14:

Solution to Exercise 4.15:
- Diminished sixth
- Perfect fourth
- Augmented fourth
- Minor second
- Major third
Solution to Exercise 4.16:
- The ratio 4:6 reduced to lowest terms is 2:3. (In other words, they are two ways of writing the same mathematical relationship. If you are more comfortable with fractions than with ratios, think of all the ratios as fractions instead. 2:3 is just two-thirds, and 4:6 is four-sixths. Four-sixths reduces to two-thirds.)
- Six and nine (6:9 also reduces to 2:3); eight and twelve; ten and fifteen; and any other combination that can be reduced to 2:3 (12:18, 14:21 and so on).
- Harmonics three and four; six and eight; nine and twelve; twelve and sixteen; and so on.
- 3:4
Solution to Exercise 4.17:
Opening both first and second valves gives the harmonic series one-and-a-half steps lower than "no valves".

Solution to Exercise 4.18:
- E flat major (3 flats):
- B flat major (2 flats)
- A flat major (4 flats)
- C minor (3 flats)
- G minor (2 flats)
- F minor (4 flats)
A minor (no sharps or flats):
- E minor (1 sharp)
- D minor (1 flat)
- C major (no sharps or flats)
- G major (1 sharp)
- F major (1 flat)
Solution to Exercise 4.19:

Solution to Exercise 4.20:
- A major adds G sharp
- E major adds D sharp
- B major adds A sharp
- F sharp major adds E sharp

Solution to Exercise 4.21:
- B minor adds C sharp
- F sharp minor adds G sharp
- C sharp minor adds D sharp

Solution to Exercise 4.22:
- E flat major adds A flat
- A flat major adds D flat
- D flat major adds G flat
- G flat major adds C flat

Solution to Exercise 4.23:

Solution to Exercise 4.24:

Assuming that octaves don't matter - as they usually don't in Western music theory, this scale shares all of its possible pitches with the scale in Figure 4.48.
Solution to Exercise 4.25:
If you can, have your teacher listen to your compositions.
- 9288 reads






