The basic principles of reinforcement, reward, and punishment have been used to help understand a variety of human behaviors (Rotter, 1945; Bandura, 1977; Miller & Dollard, 1941). 1 The general idea is that, as predicted by principles of operant learning and the law of effect, people act in ways that maximize theiroutcomes, where outcomes are defined as the presence of reinforcers and the absence of punishers.
Consider, for example, a situation known as the commons dilemma, as proposed by the ecologist Garrett Hardin (1968). 2 Hardin noted that in many European towns there was at one time a centrally located pasture, known as the commons, which was shared by the inhabitants of the village to graze their livestock. But the commons was not always used wisely. The problem was that each individual who owned livestock wanted to be able to use the commons to graze his or her own animals. However, when each group member took advantage of the c ommons by grazing many animals, the commons became overgrazed, the pasture died, and the commons was destroyed.
Although Hardin focused on the particular example of the commons, the basic dilemma of individual desires versus the benefit of the group as whole ca n also be found in many contemporary public goods issues, including the use of limited natural resources, air pollution, and public land. In large cities most people may prefer the convenience of driving their own car to work each day rather than taking public transportation. Yet this behavior uses up public goods (the space on limited roadways, crude oil reserves, and clean air). People are lured into the dilemma by short-term rewards, seemingly without considering the potential long-term costs of the behavior, such as air pollution and the necessity of building even more highways.
A social dilemma such as the commons dilemma is a situation in which thebehavior that creates themost positiveoutcomes for theindividual mayin thelong term lead to negative consequences for thegroup as a whole. The dilemmas are arranged in a way that it is easy to be selfish, because the personally beneficial choice (such as using water during a water shortage or driving to work alone in one’s own car) produces reinforcements for the individual. Furthermore, social dilemmas tend to work on a type of “time delay.” The problem is that, because the long-term negative outcome (the extinction of fish species or dramatic changes in the earth’s climate) is far away in the future and the individual benefits are occurring right now, it is difficult for an individual to see how many costs there really are. The paradox, of course, is that if everyone takes the personally selfish choice in an attempt to maximize his or her own outcomes, the long- term result is poorer outcomes for every individual in the group. Each individual prefers to make use of the public goods for himself or herself, whereas the best outcome for the group as a whole is to use the resources more slowly and wisely.
One method of understanding how individuals and groups behave in social dilemmas is to create such situations in the laboratory and observe how people react to them. The best known of these laboratory simulations is called theprisoner’s dilemma game (Poundstone, 1992). 3 This game represents a social dilemma in which thegoals of theindividual competewith thegoals of another individual (or sometimes with a group of other individuals). Like all social dilemmas, the prisoner’s dilemma assumes that individuals will generally try to maximize their own outcomes in their interactions with others.
In the prisoner’s dilemma game, the participants are shown a payoff matrixin which numbers are used to express the potential outcomes for each of the players in the game, given the decisions each player makes. The payoffs are chosen beforehand by the experimenter to create a situation that models some real-world outcome. Furthermore, in the prisoner’s dilemma game, the payoffs are normally arranged as they would be in a typical social dilemma, such that each individual is better off acting in his or her immediate self-interest, and yet if all individuals act according to their self-interests, then everyone will be worse off.
In its original form, the prisoner’s dilemma game involves a situation in which two prisoners (we’ll call them Frank and Malik) have been accused of committing a crime. The police believe that the two worked together on the crime, but they have only been able to gather enough evidence to convict each of them of a more minor offense. In an attempt to gain more evidence, and thus to be able to convict the prisoners of the larger crime, each of the prisoners is interrogated individually, with the hope that he will confess to having been involved in the more major crime, in return for a promise of a reduced sentence if he confesses first. Each prisoner can make either the cooperativechoice(which is to not confess) or the competitive choice(which is to confess).
The incentives for either confessing or not confessing are expressed in a payoff matrix such as the one shown in Figure 7.6. The top of the matrix represents the two choices that Malik might make (to either confess that he did the crime or not confess), and the side of the matrix represents the two choices that Frank might make (also to either confess or not confess). The payoffs that each prisoner receives, given the choices of each of the two prisoners, are shown in each of the four squares.
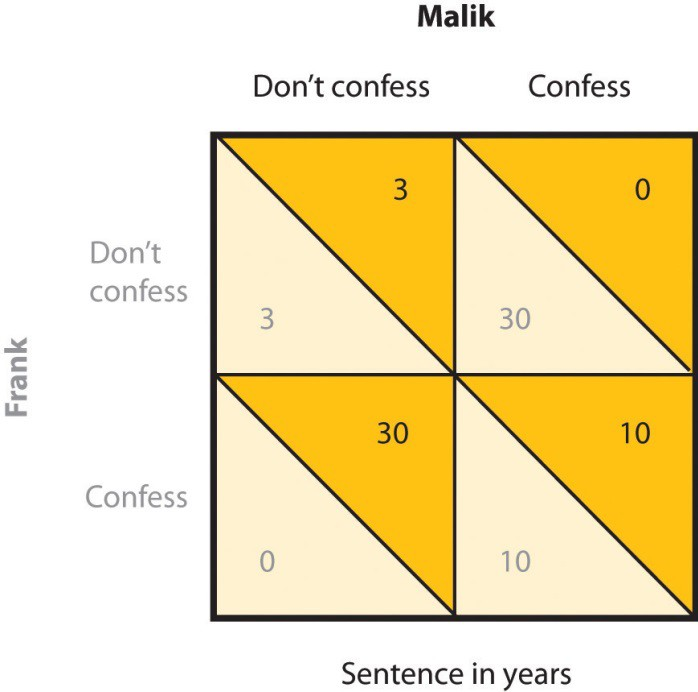
If both prisoners take the cooperative choice by not confessing (the situation represented in the upper left square of the matrix), there will be a trial, the limited available information will be used to convict each prisoner, and they each will be sentenced to a relatively short prison term of three years. However, if either of the prisoners confesses, turning “state’s evidence” against the other prisoner, then there will be enough information to convict the other prisoner of the larger crime, and that prisoner will receive a sentence of 30 years, whereas the prisoner who confesses will get off free. These outcomes are represented in the lower left and upper right squares of the matrix. Finally, it is possible that both players confess at the same time. In this case there is no need for a trial, and in return the prosecutors offer a somewhat reduced sentence (of 10 years) to each of the prisoners.
The prisoner’s dilemma has two interesting characteristics that make it a useful model of a social dilemma. For one, the prisoner’s dilemma is arranged such that a positive outcome for one player does not necessarily mean a negative outcome for the other player. If you consider again the matrix in Figure 7.6, you can see that if one player takes the cooperative choice (to not confess) and the other takes the competitive choice ( to confess), then the prisoner who cooperates loses, whereas the other prisoner wins. However, if both prisoners make the cooperative choice, each remaining quiet, then neither gains more than the other, and both prisoners receive a relatively light sentence. In this sense both players can win at the same time.
Second, the prisoner’s dilemma matrix is arranged such that each individual player is motivated to take the competitive choice, because this choice leads to a higher payoff regardless of what the other player does. Imagine for a moment that you are Malik, and you are trying to decide whether to cooperate (don’t confess) or to compete (confess). And imagine that you are not really sure what Frank is going to do. Remember the goal of the individual is to maximize outcomes. The values in the matrix make it clear that if you think that Frank is going to confess, you should confess yourself (to get 10 rather than 30 years in prison). And, it is also clear that if you think Frank is not going to confess, you should still confess (to get 0 rather than 3 years in prison). So the matrix is arranged such that the “best” alternative for each player, at least in the sense of pure reward and self-interest, is to make the competitive choice, even though in the end both players would prefer the combination in which both players cooperate to the one in which they both compete.
Although initially specified in terms of the two prisoners, similar payoff matrices can be used to predict behavior in many different types of dilemmas involving two or more parties and including choices of helping and not helping, working and loafing, and paying and not paying debts. For instance, we can use the prisoner’s dilemma to help us understand roommates living together in a house who might not want to contribute to the housework. Each of them would be better off if they relied on the other to clean the house. Yet if neither of them makes an effort to clean the house (the cooperative choice), the house becomes a mess and they will both be worse off.
KEY TAKEAWAYS
- Learning theories have been used to change behaviors in many areas of everyday life.
- Some advertising uses classical conditioning to associate a pleasant response with a product.
- Rewards are frequently and effectively used in education but must be carefully designed to be contingent on performance and to avoid undermining interest in the activity.
- Social dilemmas, such as the prisoner’s dilemma, can be understood in terms of a desire to maximize one’s outcome in a competitive relationship.
EXERCISES AND CRITICAL THINKING
- Find and share with your class some examples of advertisements that make use of classical conditioning to create positive attitudes toward products.
- Should parents use both punishment as well as reinforcement to discipline their children? On what principles of learning do you base your opinion?
- Think of a social dilemma other than one that has been discussed in this chapter, and explain people’s behavior in it in terms of principles of learning.
- 5350 reads






