Whether economists measure the marginal benefits and marginal costs of emissions or, alternatively, the marginal benefits and marginal costs of abatement, the policy implications are the same from an economic perspective. As shown in Panel (a) of Figure 18.4, applying the marginal decision rule in the case of emissions suggests that the efficient level of pollution occurs at six pounds of CO emitted per week. At any lower level, the marginal benefits of the pollution would outweigh the marginal costs. At a higher level, the marginal costs of the pollution would outweigh the marginal benefits.
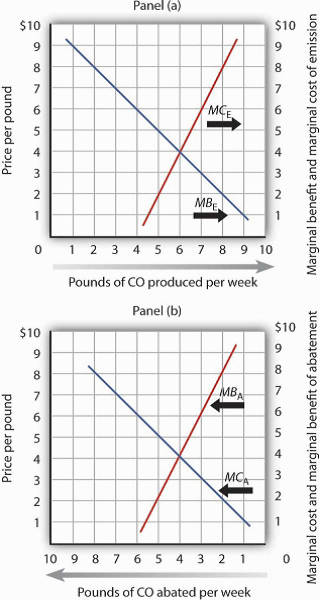
In Panel (a) we combine the marginal benefit of emissions (MBE) with the marginal cost of emissions (MCE). The efficient solution occurs at the intersection of the two curves. Here, the efficient quantity of emissions is six pounds of CO per week. In Panel (b), we have the same curves read from right to left. The marginal cost curve for emissions becomes the marginal benefit of abatement (MBA). The marginal benefit curve for emissions becomes the marginal cost of abatement (MCA). With no abatement program, emissions total ten pounds of CO per week. The efficient degree of abatement is to reduce emissions by four pounds of CO per week to six pounds per week.
As shown in Panel (b) of Figure 18.4, application of the marginal decision rule suggests that the efficient level of abatement effort is to reduce pollution by 4 pounds of CO produced per week. That is, reduce the level of pollution from the 10 pounds per week that would occur at a zero price to 6 pounds per week. For any greater effort at abating the pollution, the marginal cost of the abatement efforts would exceed the marginal benefit.
KEY TAKEAWAYS
- Pollution is related to the concept of scarcity. The existence of pollution implies that an environmental resource has alternative uses and is thus scarce.
- Pollution has benefits as well as costs; the emission of pollutants benefits people by allowing other activities to be pursued at lower costs. The efficient rate of emissions occurs where the marginal benefit of emissions equals the marginal cost they impose.
- The marginal benefit curve for emitting pollutants can also be read from right to left as the marginal cost of abating emissions. The marginal cost curve for increased emission levels can also be read from right to left as the demand curve for improved environmental quality.
- The Coase theorem suggests that if property rights are well-defined and if transactions are costless, then the private market will reach an efficient solution. These conditions, however, are not likely to be present in typical environmental situations. Even if such conditions do not exist, Coase’s arguments still yield useful insights to the mitigation of environmental problems.
- Surveys are sometimes used to measure the marginal benefit curves for emissions and the marginal cost curves for increased pollution levels. Marginal cost curves may also be inferred from other relationships. Two that are commonly used are the demand for housing and the relationship between pollution and production.
TRY IT!
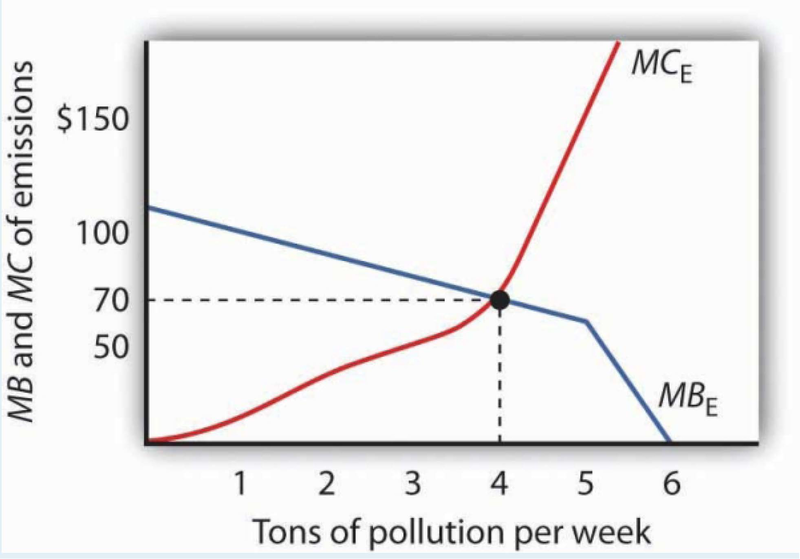
The table shows the marginal benefit to a paper mill of polluting a river and the marginal cost to residents who live downstream. In this problem assume that the marginal benefits and marginal costs are measured at (not between) the specific quantities shown.
Plot the marginal benefit and marginal cost curves. What is the efficient quantity of pollution? Explain why neither one ton nor five tons is an efficient quantity of pollution. In the absence of pollution fees or taxes, how many units of pollution do you expect the paper mill will choose to produce? Why?
| Quantity of pollution (tons per week) | Marginal benefit | Marginal cost |
| 0 | $110 | $0 |
| 1 | 100 | 8 |
| 2 | 90 | 20 |
| 3 | 80 | 35 |
| 4 | 70 | 70 |
| 5 | 60 | 150 |
| 6 | 0 | 300 |
Case in Point: Estimating a Demand Curve for Environmental Quality
How do economists estimate demand curves for environmental quality? One recent example comes from work by Louisiana State University economist David M. Brasington and Auburn University economist Diane Hite. Using data from Ohio’s six major metropolitan areas (Akron, Cincinnati, Cleveland, Columbus, Dayton, and Toledo), the economists studied the relationship between house prices and the distance between individual houses and hazardous waste sites. From this, they were able to estimate the demand curve for environmental quality—at least in terms of the demand for locations farther from environmental hazards.
The economists used actual real estate transactions in 1991 to get data on house prices. In that year, there were 1,192 hazardous sites in the six metropolitan areas. The study was based on 44,255 houses. The median distance between a house and a hazardous site was 1.08 miles. The two economists found, as one would expect, that house prices were higher the greater the distance between the house and a hazardous site. All other variables unchanged, increasing the distance from a house to a hazardous site by 10% increased house value by 0.3%.
Other characteristics of the demand curve shed light on the relationship between environmental quality and other goods. For example, the study showed that people substitute house size for environmental quality. A house closer to a hazardous waste site is cheaper; people take advantage of the lower price of such sites to purchase larger houses.
While house size and environmental quality were substitutes, school quality, measured by student scores on achievement tests, was a complement. If the price of school quality were to fall by 10%, household would buy 8% more environmental quality. The cross-price elasticity between environmental quality and school quality was thus estimated to be −0.80.
There is no marketplace for environmental quality. Estimating the demand curve for such quality requires economists to examine other data to try to infer what the demand curve is. The study by Professors Brasington and Hite illustrates the use of an examination of an actual market, the market for houses, to determine characteristics of the demand curve for environmental quality.
Source: David M. Brasington and Diane Hite, “Demand for Environmental Quality: A Spatial Hedonic Analysis,” Regional Science & Urban Economics, 35(1) (January 2005): 57–82.
ANSWER TO TRY IT! PROBLEM
The efficient quantity of pollution is four tons per week. At one ton of pollution, the marginal benefit exceeds the marginal cost. If the paper mill expands production, the additional pollution generated leads to additional benefits for it that are greater than the additional cost to the residents nearby. At five tons, the marginal cost of polluting exceeds the marginal benefit. Reducing production, and hence pollution, brings the marginal costs and benefits closer.
In the absence of any fees, taxes, or other charges for its pollution, the paper mill will likely choose to generate six tons per week, where the marginal benefit has fallen to zero.
- 11950 reads






