One method of understanding how individuals and groups behave in social dilemmas is to create such situations in the laboratory and observe how people react to them. The best known of these laboratory simulations is called the prisoner’s dilemma game (Poundstone, 1992). The prisoner’s dilemma game is a laboratory simulation that models a social dilemma in which the goals of the individual compete with the goals of another individual (or sometimes with a group of other individuals). Like all social dilemmas, the prisoner’s dilemma makes use of the assumptions of social learning approaches to behavior that assume that individuals will try to maximize their own outcomes in their interactions with others.
In the prisoner’s dilemma, the participants are shown a payoff matrix in which numbers are used to express the potential outcomes for the each of the players in the game, given the decisions made by each player. The payoffs are chosen beforehand by the experimenter to create a situation that models some real-world outcome. Furthermore, in the prisoner’s dilemma, the payoffs are normally arranged as they would be in a typical social dilemma, such that each individual is better off acting in his or her immediate self-interest, and yet if all individuals act according to their self-interest, then everyone will be worse off.
In its original form, the prisoner’s dilemma involves a situation in which two prisoners (we’ll call them Frank and Malik) have been accused of committing a crime. The police have determined that the two worked together on the crime, but they have only been able to gather enough evidence to convict each of them of a more minor offense. In an attempt to gain more evidence and thus to be able to convict the prisoners of the larger crime, each prisoner is interrogated individually, with the hope that he will confess to having been involved in the more major crime in return for a promise of a reduced sentence if he confesses first. Each prisoner can make either the cooperative choice (which is to not confess) or the competitive choice (which is to confess).
The incentives for either confessing or not confessing are expressed in a payoff matrix such as the one shown in Figure 12.5. The top of the matrix represents the two choices that Malik might make (either to confess that he did the crime or to not confess), and the side of the matrix represents the two choices that Frank might make (also to either confess or not confess). The payoffs that each prisoner receives, given the choices of each of the two prisoners, are shown in each of the four squares.
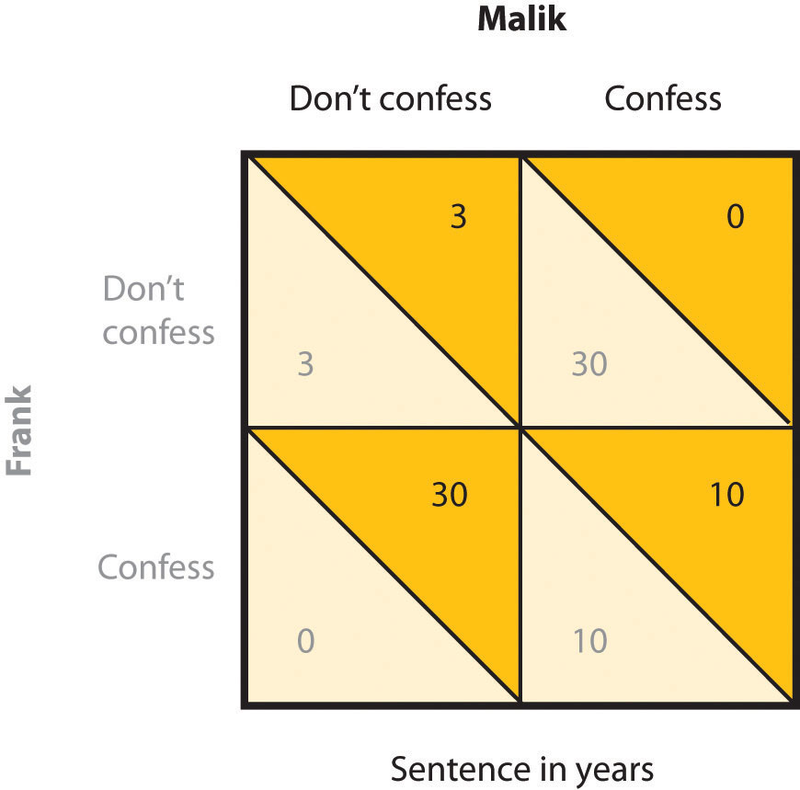
In the prisoner’s dilemma, two suspected criminals are interrogated separately. The payoff matrix indicates the outcomes for each prisoner, measured as the number of years each is sentenced to prison, as a result of each combination of cooperative (don’t confess) and competitive (confess) decisions. Outcomes for Malik are in the darker color, and outcomes for Frank are in lighter color.
If both prisoners take the cooperative choice by not confessing (the situation represented in the upper left square of the matrix), there will be a trial, the limited available information will be used to convict each prisoner, and each will be sentenced to a relatively short prison term of three years. However, if either of the prisoners confesses, turning “state’s evidence” against the other prisoner, then there will be enough information to convict the other prisoner of the larger crime, and that prisoner will receive a sentence of 30 years, whereas the prisoner who confesses will get off free. These outcomes are represented in the lower left and upper right squares of the matrix. Finally, it is possible that both players confess at the same time. In this case, there is no need for a trial, and in return, the prosecutors offer a somewhat reduced sentence (of 10 years) to each of the prisoners.
- 4428 reads






