In addition to the prisoner’s dilemma, social dilemmas have been studied using games in which a group of individuals share a common pool of resources. In these resource dilemma games, the participants may extract or harvest resources from the pool, and it is to their individual advantage to do so. Furthermore, as the resources are used, the pool can replenish itself through a fixed schedule, which will allow the individuals to continue to harvest over long periods of time. Optimal use of the resource involves keeping the pool level up and harvesting only as much as will be replenished in the given time period. Overuse of the pool provides immediate gain for the individuals but has a long-term cost in the inability to make harvests at a later time.
In one version of a resource dilemma game (Edney, 1979), the participants sit around a bowl of metal nuts, and the goal is to get as many nuts as one can. The experimenter adds nuts to the bowl so that the number of nuts in the bowl doubles every 10 seconds. However, the individual players are also motivated to harvest nuts for themselves and are allowed to take out as many nuts as they like at any time. In Edney’s research, rather than cooperating and watching the pool grow, the participants almost immediately acted in their self-interest, grabbing the nuts from the bowl. In fact, Edney reported that 65% of the groups never got to the first 10-second replenishment!
Research Focus: The Trucking Game
Another example of a laboratory simulation that has been used to study conflict is the trucking game. In the original research (Deutsch & Krauss, 1960), pairs of women played the trucking game. Each woman was given $4 to begin with and was asked to imagine herself as the owner of one of two trucking companies (Acme or Bolt) that carried merchandise over the roads shown in Figure 12.6. Each time either player’s truck reached the destination on the opposite side of the board, she earned 60 cents, minus operating costs (1 cent for each second taken by the trip). However, the game was also arranged to create the potential for conflict. Each participant wanted to travel on the main road in order to get to the destination faster, but this road was arranged to be so narrow that only one truck could pass at a time. Whenever the two trucks met each other on this narrow road, one of them was eventually forced to back up. Thus there are two choices to getting to the destination. The players had to either take the long, winding roads, thus eliminating their profits (each player would lose 10 cents on each trip if they were forced to take the long road) or figure out a way to share the use of the one-lane road.
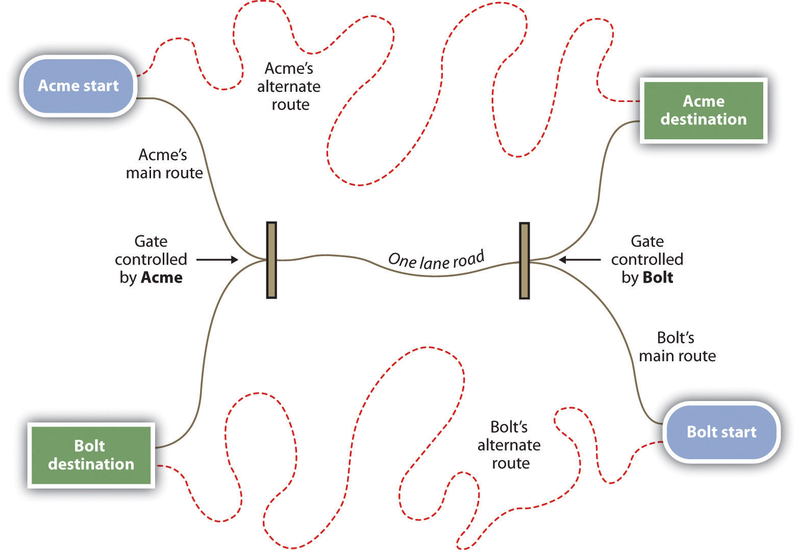
Deutsch and Krauss made the game even more interesting by creating experimental conditions in which either or both of the truck company owners had a gate that controlled access to the road.
In the unilateral-threat condition, only Acme had a gate. Thus if Bolt attempted to use the main road, Acme could close the gate, forcing Bolt to back up and enabling Acme to reopen the gate
and proceed quickly to the destination. In the bilateral-threat condition, both sides had gates, whereas in the no-threat condition, there were no gates.
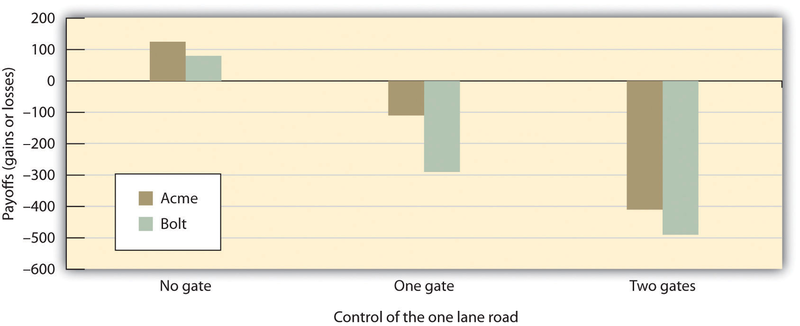
As shown in Figure 12.7,
participants without gates soon learned to share the one-lane road, and, on average, each made a profit. However, threat in the form of a gate produced conflict and led to fewer profits,
although in many cases the participants learned to deal with these problems over time and improved their payoffs as the game went on (Lawler, Ford, & Blegen, 1988; Shomer, Davis, &
Kelley, 1966). Participants lost the most money in the bilateral-threat condition in which both sides were given gates that they could control. In this situation, conflict immediately
developed, and there were standoffs on the middle road that wasted time and prevented either truck from moving.
Two results of this study are particularly surprising. First, in the unilateral threat condition, both players (including Acme, who had control of the gate) made less money than did those in
the no-threat condition (although it is true that in this condition, Acme did lose less than Bolt). Thus being able to threaten the other was not successful for generating overall profits.
Second, in the conditions in which both individuals had gates, both individuals actually did worse than they did when only one individual had a gate. Thus when an opponent is able to threaten
you, it may be to your benefit to not return with a threat of your own—the ability to counteract the threats of your partner may not always help you but rather may produce even more conflict
and losses for both parties.
- 6990 reads






