The Sinusoid

Available under Creative Commons-ShareAlike 4.0 International License.

The most ubiquitous and important signal in electrical engineering is the sinusoid.

Sine Definition

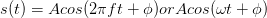
A is known as the sinusoid's amplitude, and determines the sinusoid's size. The amplitude conveys the sinusoid's physical units (volts, lumens, etc). The frequencyf has units of Hz (Hertz) or s^-1, and determines how rapidly the sinusoid oscillates per unit time. The temporal variable t always has units of seconds, and thus the frequency determines how many oscillations/second the sinusoid has. AM radio stations have carrier frequencies of about 1 MHz (one mega-hertz or 106 Hz), while FM stations have carrier frequencies of about 100 MHz. Frequency can also be expressed by the symbol ω, which has units of radians/second. Clearly, 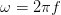. In communications, we most often express frequency in Hertz. Finally, φ is the phase, and determines the sine wave's behavior at the origin (t =0). It has units of radians, but we can express it in degrees, realizing that in computations we must convert from degrees to radians. Note that if 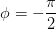 , the sinusoid corresponds to a sine function, having a zero value at the origin.

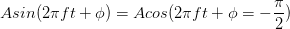
Thus, the only difference between a sine and cosine signal is the phase; we term either a sinusoid.

We can also define a discrete-time variant of the sinusoid: 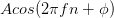. Here, the independent variable is n and represents the integers. Frequency now has no dimensions, and takes on values between 0 and 1.