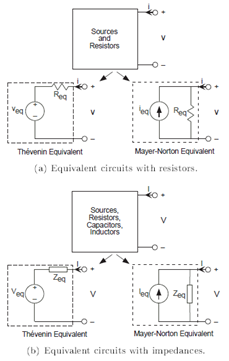
When we have circuits with capacitors and/or inductors as well as resistors and sources, Thevenin and Mayer-Norton equivalent circuits can still be defined by using impedances and complex amplitudes for voltage and currents. For any circuit containing sources, resistors, capacitors, and inductors, the input-output relation for the complex amplitudes of the terminal voltage and current is
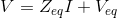
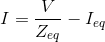
with Veq = ZeqIeq. Thus, we have Thevenin and Mayer-Norton equivalent circuits as shown in Figure 3.27.
Equivalent Circuits
Example 3.4
Simple RC Circuit
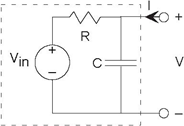
Let's find the Thevenin and Mayer-Norton equivalent circuits for Figure 3.28 (Simple RC Circuit). The open-circuit voltage and short-circuit current techniques still work, except we use
impedances and complex amplitudes. The open-circuit voltage corresponds to the transfer function we have already found. When we short the terminals, the capacitor no longer has any effect on
the circuit, and the short-circuit current Isc equals 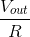 . The equivalent impedance can be found by setting the source to zero, and finding the impedance using series and parallel
combination rules. In our case, the resistor and capacitor are in parallel once the voltage source is removed (setting it to zero amounts to replacing it with a short-circuit). Thus,
. The equivalent impedance can be found by setting the source to zero, and finding the impedance using series and parallel
combination rules. In our case, the resistor and capacitor are in parallel once the voltage source is removed (setting it to zero amounts to replacing it with a short-circuit). Thus,
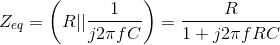
Consequently, we have
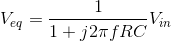
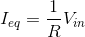
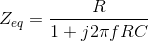
Again, we should check the units of our answer. Note in particular that j2πfRC must be dimensionless. Is it?
- 3512 reads






