Wireless channels exploit the prediction made by Maxwell's equation that electromagnetic fields propagate in free space like light. When a voltage is applied to an antenna, it creates an electromagnetic field that propagates in all directions (although antenna geometry affects how much power flows in any given direction) that induces electric currents in the receiver's antenna. Antenna geometry determines how energetic a field a voltage of a given frequency creates. In general terms, the dominant factor is the relation of the antenna's size to the field's wavelength. The fundamental equation relating frequency and wavelength for a propagating wave is
λf = c
Thus, wavelength and frequency are inversely related: High frequency corresponds to small wavelengths. For example, a 1 MHz electromagnetic field has a wavelength of 300 m. Antennas having a size or distance from the ground comparable to the wavelength radiate fields most efficiently. Consequently, the lower the frequency the bigger the antenna must be. Because most information signals are baseband signals, having spectral energy at low frequencies, they must be modulated to higher frequencies to be transmitted over wireless channels.
For most antenna-based wireless systems, how the signal diminishes as the receiver moves further from the transmitter derives by considering how radiated power changes with distance from the transmitting antenna. An antenna radiates a given amount of power into free space, and ideally this power propagates without loss in all directions. Considering a sphere centered at the transmitter, the total power, which is found by integrating the radiated power over the surface of the sphere, must be constant regardless of the sphere's radius. This requirement results from the conservation of energy. Thus, if p (d) represents the power integrated with respect to direction at a distance d from the antenna, the total power will be p (d)4πd2 . For this quantity to be a constant, we must have
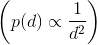
which means that the received signal amplitude AR must be proportional to the transmitter's amplitude AT and inversely related to distance from the transmitter.
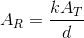
(6.17)
for some value of the constant k. Thus, the further from the transmitter the receiver is located, the weaker the received signal. Whereas the attenuation found in wireline channels can be controlled by physical parameters and choice of transmission frequency, the inverse-distance attenuation found in wireless channels persists across all frequencies.
Exercise 6.4.1
Why don't signals attenuate according to the inverse-square law in a conductor? What is the difference between the wireline and wireless cases?
The speed of propagation is governed by the dielectric constant µ0 and magnetic permeability E0 of free space.
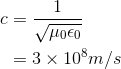
(6.18)
Known familiarly as the speed of light, it sets an upper limit on how fast signals can propagate from one place to another. Because signals travel at a finite speed, a receiver senses a transmitted signal only after a time delay inversely related to the propagation speed:
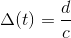
(6.19)
At the speed of light, a signal travels across the United States in 16 ms, a reasonably small time delay. If a lossless (zero space constant) coaxial cable connected the East and West coasts, this delay would be two to three times longer because of the slower propagation speed.
- 瀏覽次數:2508






