The voltage law says that the sum of voltages around every closed loop in the circuit must equal zero. A closed loop has the obvious defnition: Starting at a node, trace a path through the circuit that returns you to the origin node. KVL expresses the fact that electric fields are conservative: The total work performed in moving a test charge around a closed path is zero. The KVL equation for our circuit is
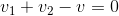
In writing KVL equations, we follow the convention that an element's voltage enters with a plus sign when traversing the closed path, we go from the positive to the negative of the voltage's defnition.
For the example circuit (Simple circult), we have three v-i relations, two KCL equations, and one KVL equation for solving for the circuit's six voltages and currents.
v-i:
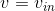
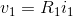
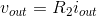
KCL:
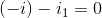
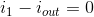
KVL:
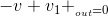
We have exactly the right number of equations! Eventually, we will discover shortcuts for solving circuit problems; for now, we want to eliminate all the variables but vout
and determine how it depends on vin and on resistor values. The KVL equation can be rewritten as vin = v1 + vout . Substituting into it the
resistor's v-i relation, we have vin = R1i1 +
R2iout . Yes, we temporarily eliminate the quantity we seek. Though not obvious, it is the simplest way to solve the equations. One
of the KCL equations says i1 = iout, which means that vin =
R1iout + R2iout =(R1 + R2)
iout. Solving for the current in the output resistor, we have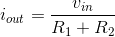 
. We have now solved the circuit: We have expressed one voltage or current in terms of
R1+R2sources and circuit-element values. To find any other circuit quantities, we can back substitute this answer into our original
equations or ones we developed along the way. Using the v-i relation for the output resistor, we obtain the quantity we seek.
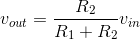
Exercise 3.4.2
Referring back to Figure 3.6, a circuit should serve some useful purpose. What kind of system does our circuit realize and, in terms of element values, what are the system's parameter(s)?
- 3053 reads
