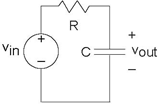
Let's consider a circuit having something other than resistors and sources. Because of KVL, we know that vin= vR+
vout. The current through the capacitor is given by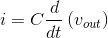 
, and this current equals that passing through the resistor. Substituting vR = Ri into the KVL equation and using the v-i relation for the capacitor, we arrive at
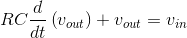
The input-output relation for circuits involving energy storage elements takes the form of an ordinary differential equation, which we must solve to determine what the output voltage is for a given input. In contrast to resistive circuits, where we obtain an explicit input-output relation, we now have an implicit relation that requires more work to obtain answers.
At this point, we could learn how to solve differential equations. Note first that even finding the differential equation relating an output variable to a source is often very tedious. The parallel and series combination rules that apply to resistors don't directly apply when capacitors and inductors occur. We would have to slog our way through the circuit equations, simplifying them until we fnally found the equation that related the source(s) to the output. At the turn of the twentieth century, a method was discovered that not only made fnding the differential equation easy, but also simplifed the solution process in the most common situation. Although not original with him, Charles Steinmetzl9 presented the key paper describing the impedance approach in 1893. It allows circuits containing capacitors and inductors to be solved with the same methods we have learned to solved resistor circuits. To use impedances, we must master complex numbers. Though the arithmetic of complex numbers is mathematically more complicated than with real numbers, the increased insight into circuit behavior and the ease with which circuits are solved with impedances is well worth the diversion. But more importantly, the impedance concept is central to engineering and physics, having a reach far beyond just circuits.
- 瀏覽次數：1619
