In the Huffman code, the bit sequences that represent individual symbols can have differing lengths so the bitstream index m does not increase in lock step with the symbol-valued signal's index
n. To capture how often bits must be transmitted to keep up with the source's production of symbols, we can only compute averages. If our source code averages 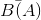 bits/symbol and symbols are produced at a rate R, the average bit rate
equals
bits/symbol and symbols are produced at a rate R, the average bit rate
equals 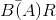 , and this quantity determines the bit
interval duration T.
, and this quantity determines the bit
interval duration T.
Exercise 6.23.1
Calculate what the relation between T and the average bit rate 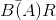 is.
is.
A subtlety of source coding is whether we need "commas" in the bitstream. When we use an unequal number of bits to represent symbols, how does the receiver determine when symbols begin and end? If you created a source code that required a separation marker in the bitstream between symbols, it would be very inefficient since you are essentially requiring an extra symbol in the transmission stream.
NOTE: A good example of this need is the Morse Code: Between each letter, the telegrapher needs to insert a pause to inform the receiver when letter boundaries occur.
As shown in this example (Compression and the Huffman Code), no commas are placed in the bitstream, but you can unambiguously decode the sequence of symbols from the bitstream. Huffman showed that his (maximally efficient) code had the prefix property: No code for a symbol began another symbol's code. Once you have the prefix property, the bitstream is partially self-synchronizing: Once the receiver knows where the bitstream starts, we can assign a unique and correct symbol sequence to the bitstream.
Exercise 6.23.2
Sketch an argument that prefx coding, whether derived from a Hufman code or not, will provide unique decoding when an unequal number of bits/symbol are used in the code.
However, having a prefx code does not guarantee total synchronization: After hopping into the middle of a bitstream, can we always find the correct symbol boundaries? The self-synchronization issue does mitigate the use of efcient source coding algorithms.
Exercise 6.23.3
Show by example that a bitstream produced by a Hufman code is not necessarily self-synchronizing. Are fxed-length codes self synchronizing?
Another issue is bit errors induced by the digital channel; if they occur (and they will), synchronization can easily be lost even if the receiver started "in synch" with the source. Despite the small probabilities of error ofered by good signal set design and the matched filter, an infrequent error can devastate the ability to translate a bitstream into a symbolic signal. We need ways of reducing reception errors without demanding that pe be smaller.
Example 6.4
The first electrical communications system the telegraph was digital. When first deployed in 1844, it communicated text over wireline connections using a binary code the Morse code to represent individual letters. To send a message from one place to another, telegraph operators would tap the message using a telegraph key to another operator, who would relay the message on to the next operator, presumably getting the message closer to its destination. In short, the telegraph relied on a network not unlike the basics of modern computer networks. To say it presaged modern communications would be an understatement. It was also far ahead of some needed technologies, namely the Source Coding Theorem. The Morse code, shown in Figure 6.19, was not a prefix code. To separate codes for each letter, Morse code required that a space a pause be inserted between each letter. In information theory, that space counts as another code letter, which means that the Morse code encoded text with a three-letter source code: dots, dashes and space. The resulting source code is not within a bit of entropy, and is grossly inefficient (about 25%). Figure 6.19 shows a Huffman code for English text, which as we know is efficient.
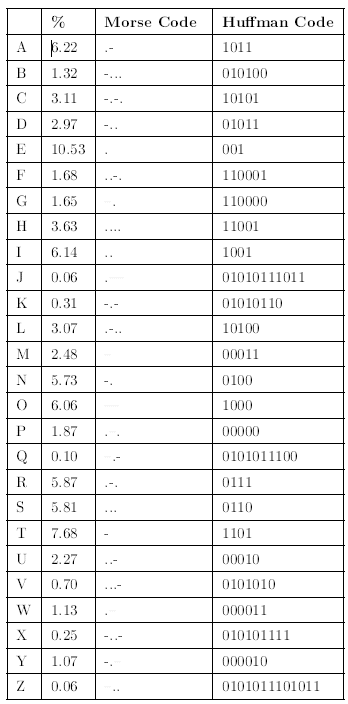
Morse and Huffman Codes for American-Roman Alphabet. The % column indicates the average probability (expressed in percent) of the letter occurring in English. The entropy H (A) of the this source is 4.14 bits. The average Morse codeword length is 2.5 symbols. Adding one more symbol for the letter separator and converting to bits yields an average codeword length of 5.56 bits. The average Huffman codeword length is 4.35 bits.
- 瀏覽次數:3446






