The notion of the square root of −1 originated with the quadratic formula: the solution of certain quadratic equations mathematically exists only if the so-called imaginary quantity 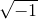 could be defined. Euler first used i for the imaginary unit but that notation did not
take hold until roughly Ampere's time. Ampere3 used the symbol i to denote current (intensite de current). It wasn't until the twentieth century that the importance of complex numbers to
circuit theory became evident. By then, using i for current was entrenched and electrical engineers chose j for writing complex numbers.
could be defined. Euler first used i for the imaginary unit but that notation did not
take hold until roughly Ampere's time. Ampere3 used the symbol i to denote current (intensite de current). It wasn't until the twentieth century that the importance of complex numbers to
circuit theory became evident. By then, using i for current was entrenched and electrical engineers chose j for writing complex numbers.
An imaginary number has the form 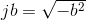 .A
complex number, z, consists of the ordered pair (a,b), a is the real component and b is the imaginary component (the j is suppressed because the
imaginary component of the pair is always in the second position). The imaginary number jb equals (0,b). Note that a and b are real-valued numbers.
.A
complex number, z, consists of the ordered pair (a,b), a is the real component and b is the imaginary component (the j is suppressed because the
imaginary component of the pair is always in the second position). The imaginary number jb equals (0,b). Note that a and b are real-valued numbers.
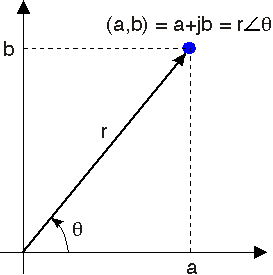
Figure 2.1 shows that we can locate a complex number in what we call the complex plane. Here, a, the real part, is the x-coordinate and b, the imaginary part, is the y-coordinate.
From analytic geometry, we know that locations in the plane can be expressed as the sum of vectors, with the vectors corresponding to the x and y directions. Consequently, a complex number z can be expressed as the (vector) sum z = a + jb where j indicates the y-coordinate. This representation is known as the Cartesian form of z. An imaginary number can't be numerically added to a real number; rather, this notation for a complex number represents vector addition, but it provides a convenient notation when we perform arithmetic manipulations.
Some obvious terminology. The real part of the complex number z = a + jb, written as Re (z), equals a. We consider the real part as a function that works by selecting that component of a complex number not multiplied by j. The imaginary part of z, Im (z), equals b: that part of a complex number that is multiplied by j. Again, both the real and imaginary parts of a complex number are real-valued.
The complex conjugate of z, written as z *, has the same real part as z but an imaginary part of the opposite sign.
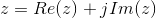
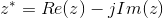
Using Cartesian notation, the following properties easily follow.
- If we add two complex numbers, the real part of the result equals the sum of the real parts and the imaginary part equals the sum of the imaginary parts. This property follows from the laws of vector addition.
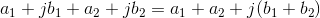
- The product of j and a real number is an imaginary number: ja. The product of j and an imaginary number is a real number: j (jb)= −b because j2 = −1. Consequently, multiplying a complex number by j rotates the number's position by 90 degrees.
Exercise 2.1.1
Use the Definition of addition to show that the real and imaginary parts can be expressed as a sum/diference of a complex number and its conjugate.
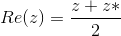 and
and 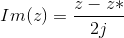
Complex numbers can also be expressed in an alternate form, polar form, which we will find quite useful. Polar form arises arises from the geometric interpretation of complex numbers. The Cartesian form of a complex number can be re-written as
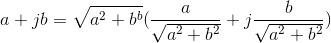
By forming a right triangle having sides a and b, we see that the real and imaginary parts correspond to the cosine and sine of the triangle's base angle. We thus obtain the polar form for complex numbers.
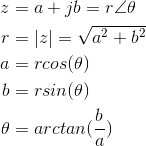
The quantity r is known as the magnitude of the complex number z, and is frequently written as |z|. The quantity θ is the complex number's angle. In using the arc-tangent formula to find the angle, we must take into account the quadrant in which the complex number lies.
Exercise 2.1.2
Convert 3 − 2j to polar form.
- 4831 reads






