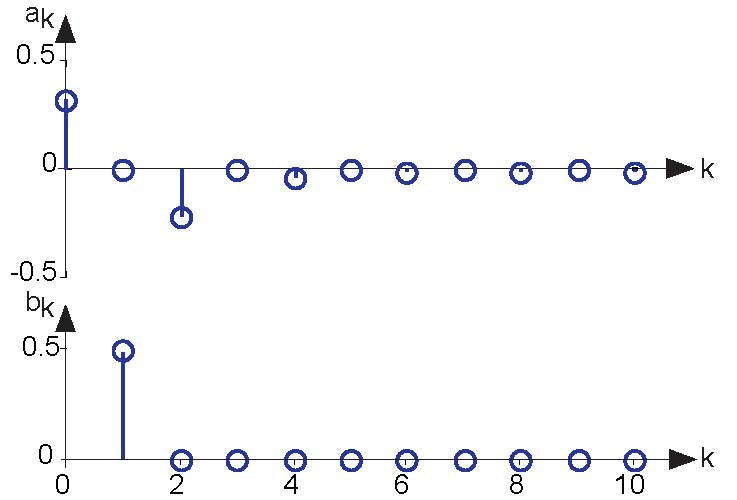
A periodic signal, such as the half-wave rectified sinusoid, consists of a sum of elemental sinusoids. A plot of the Fourier coefficients as a function of the frequency index, such as shown in
Figure 4.3 (Fourier Series spectrum of a half-wave rectified sine wave), displays the signal's spectrum. The word "spectrum" implies that the independent variable,
here k, corresponds somehow to frequency. Each coefficient is directly related to a sinusoid having a frequency of 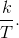 Thus, if we half-wave rectified a 1 kHz sinusoid, k =1 corresponds to 1 kHz, k =2 to 2 kHz,
etc.
Thus, if we half-wave rectified a 1 kHz sinusoid, k =1 corresponds to 1 kHz, k =2 to 2 kHz,
etc.
A subtle, but very important, aspect of the Fourier spectrum is its uniqueness: You can unambiguously find the spectrum from the signal (decomposition (4.15)) and the signal from the spectrum (composition). Thus, any aspect of the signal can be found from the spectrum and vice versa. A signal's frequency domain expression is its spectrum. A periodic signal can be defined either in the time domain (as a function) or in the frequency domain (as a spectrum).
A fundamental aspect of solving electrical engineering problems is whether the time or frequency domain provides the most understanding of a signal's properties and the simplest way of manipulating it. The uniqueness property says that either domain can provide the right answer. As a simple example, suppose we want to know the (periodic) signal's maximum value. Clearly the time domain provides the answer directly. To use a frequency domain approach would require us to find the spectrum, form the signal from the spectrum and calculate the maximum; we're back in the time domain!
Another feature of a signal is its average power. A signal's instantaneous power is defined to be its square. The average power is the average of the instantaneous power over some time interval. For a periodic signal, the natural time interval is clearly its period; for nonperiodic signals, a better choice would be entire time or time from onset. For a periodic signal, the average power is the square of its root-mean-squared (rms) value. We define the rms value of a periodic signal to be
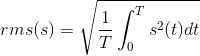 (4.20)
(4.20)
and thus its average power is
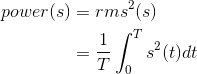
Exercise 4.4.1
What is the rms value of the half-wave rectified sinusoid?
To find the average power in the frequency domain, we need to substitute the spectral representation of the signal into this expression.
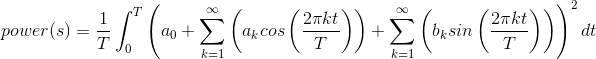
The square inside the integral will contain all possible pairwise products. However, the orthogonality properties (4.12) say that most of these crossterms integrate to zero. The survivors leave a rather simple expression for the power we seek.
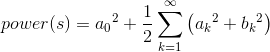
It could well be that computing this sum is easier than integrating the signal's square. Furthermore, the contribution of each term in the Fourier series toward representing the signal can be
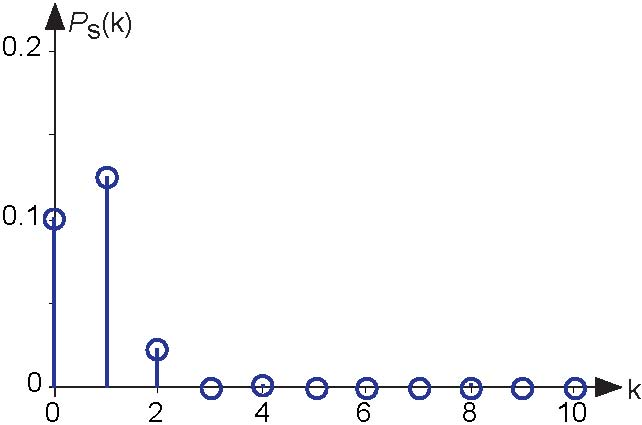
measured by its contribution to the signal's average power. Thus, the power contained in a signal at its kth harmonic is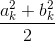 . The power spectrum, Ps (k), such as shown inFigure 4.4, plots each harmonic's contribution to the total power.
. The power spectrum, Ps (k), such as shown inFigure 4.4, plots each harmonic's contribution to the total power.
Exercise 4.4.2
In high-end audio, deviation of a sine wave from the ideal is measured by the total harmonic distortion, which equals the total power in the harmonics higher than the first compared to power in the fundamental. Find an expression for the total harmonic distortion for any periodic signal. Is this calculation most easily performed in the time or frequency domain?
- 瀏覽次數:3963






