Decibels

Available under Creative Commons-ShareAlike 4.0 International License.

The decibel scale expresses amplitudes and power values logarithmically. The definitions for these differ, but are consistent with each other.

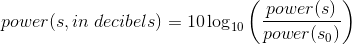
$power(s, in \; decibels) = 10\log_{10} \left ( \frac{power(s)}{power(s_{0})} \right )$

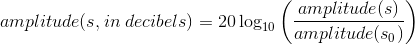
$amplitude(s,in\;decibels)=20\log_{10}\left ( \frac{amplitude(s)}{amplitude(s_{0})} \right )$

(7.1)

Here power (s₀) and amplitude (s₀) represent a reference power and amplitude, respectively. Quantifying power or amplitude in decibels essentially means that we are comparing quantities to a standard or that we want to express how they changed. You will hear statements like "The signal went down by 3 dB" and "The filter's gain in the stopband is -60" (Decibels is abbreviated dB.).

Exercise 7.1.1

The prefix "deci" implies a tenth; a decibel is a tenth of a Bel. Who is this measure named for?

The consistency of these two definitions arises because power is proportional to the square of amplitude:

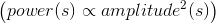
$\left ( power(s)\propto amplitude^{2}(s) \right )$

(7.2)

Plugging this expression into the Definition for decibels, we find that

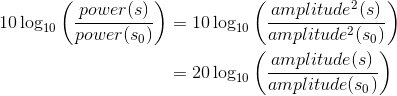
$\begin{align*} 10\log_{10}\left ( \frac{power(s)}{power(s_{0})} \right )&=10\log_{10}\left ( \frac{amplitude^{2}(s)}{amplitude^{2}(s_{0})} \right )\\ &=20\log_{10}\left ( \frac{amplitude(s)}{amplitude(s_{0})} \right )\\\end{align*}$

(7.3)

Because of this consistency, stating relative change in terms of decibels is unambiguous. A factor of 10 increase in amplitude corresponds to a 20 dB increase in both amplitude and power!

Table 7.1 Decibel table Common values for the decibel. The decibel values for all but the powers of ten are approximate, but are accurate to a decimal place.
Power Ratio	dB
1	0
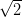
$\sqrt{2}$	1.5
2	3
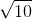
$\sqrt{10}$	5
4	6
5	7
8	9
10	10
0.1	-10

The accompanying table provides "nice" decibel values. Converting decibel values back and forth is fun, and tests your ability to think of decibel values as sums and/or differences of the well-known values and of ratios as products and/or quotients. This conversion rests on the logarithmic nature of the decibel scale.

For example, to find the decibel value for 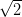$\sqrt{2}$ we halve the decibel value for 2; 26 dB equals 10 + 10 + 6 dB that corresponds to a ratio of 10 × 10 × 4 = 400. Decibel quantities add; ratio values multiply.

One reason decibels are used so much is the frequency-domain input-output relation for linear systems: Y (f)= X (f) H (f) . Because the transfer function multiplies the input signal's spectrum, to find the output amplitude at a given frequency we simply add the filter's gain in decibels (relative to a reference of one) to the input amplitude at that frequency. This calculation is one reason that we plot transfer function magnitude on a logarithmic vertical scale expressed in decibels.

瀏覽次數：1584

您在這裡

Decibels