Available under Creative Commons-ShareAlike 4.0 International License.
The unit step function (Figure 2.4) is denoted by u (t), and is defined to be
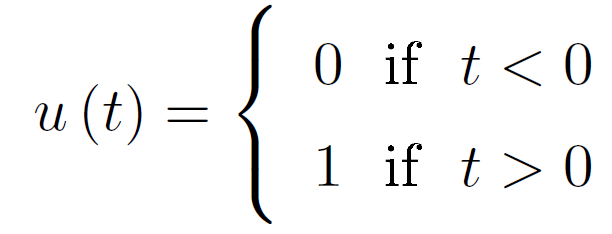
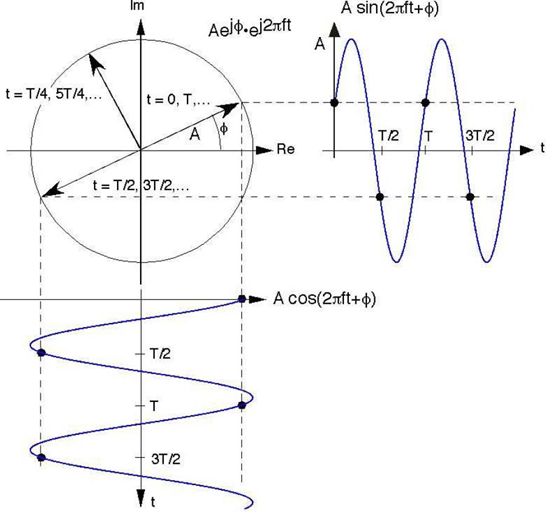
Figure 2.2 The complex exponential
Graphically, the complex exponential scribes a circle in the complex plane as time evolves. Its real and imaginary parts are sinusoids. The rate at which the signal goes around the circle is
the frequency f and the time taken to go around is the period T . A fundamental relationship is T = f 1 .
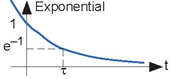
Figure 2.3 The real exponential.

Figure 2.4 The unit step.
Caution: This signal is discontinuous at the origin. Its value at the origin need not be defined, and doesn't matter in signal theory.
This kind of signal is used to describe signals that "turn on" suddenly. For example, to mathematically represent turning on an oscillator, we can write it as the product of a sinusoid and a step: s (t)= Asin (2πft) u (t).
- 瀏覽次數:2385






