Duals: a symmetry between ∧, ∨ mediated by ¬.
Looking at the provided propositional equivalences (Propositional equivalences), you should notice a strong similarity between those for ∨ and those for ∧. Take any equivalence, swap ∨s and ∧s, swap trues and falses, and you'll have another equivalencel For instance, there are two favors of DeMorgan's law, which are just duals of each other:
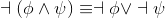
|
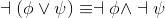
|
ASIDE: In terms of circuit diagrams, we can change each AND gate to an OR gate and add negation-bubbles to each gate's inputs and outputs. The principle of duality asserts that this operation yields an equivalent circuit.
The idea of duality is more general than this. For example, polyhedra have a natural duall5 of interchanging the role of vertices and faces.
- 2700 reads






