What about adding functions, to our language, in addition to relations? Well, functions are just a way of relating input(s) to an output. For example, 3 and 9 are related by the square function, as are 9 and 81, and 0,0. Is any binary relation a function? No, for instance {(9, 81) , (9, 17)} is not a function, because there is no unique output related to the input 9.
How can we enforce uniqueness? The following sentence asserts that for each element x of the domain, R associates at most one value with x: For all x, y and z of the domain,
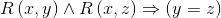
This is a common trick, for to describe uniqueness: if y and z each have some property, then they must be equal. (We have not yet specified that for every element of the domain, there is at least one element associated with it; we'll get to that later.)
Exercise 3.3.1
We just used a binary relation to model a unary function. Carry on this idea, by using a ternary relation to start to model a binary function. In particular, write a formula stating that for every pair of elements w, x in the domain, the relation S associates at most one value with that pair.
- 1978 reads






