A long outstanding problem was that of Euclid's parallel postulate: Given a line and a point not on the line, how many lines parallel to the first go through that point? Euclid took this as an axiom (unable to prove that it followed from his other axioms). Non-Euclidean geometries of Lobachevsky and Riemann took different postulates, and got different geometries. However, it was not clear whether these geometries were sound whether one could derive two different results that were inconsistent with each other.
Henri Poincare developed an ingenious method for showing that certain non-Euclidean geometries are consistent or at least, as consistent as Euclidean geometry. Remember that in Euclidean geometry, the concepts "point" and "line" are left undefined, and axioms are built on top of them (e.g., "two different lines have at most one point in common"). While it's usually left to common sense to interpret "point", "line", and "a point is on a line", any interpretation which satisfies the axioms means that all theorems of geometry will hold.
The Poincare disc is one such interpretation: "point" is taken to mean "a point in the interior of the unit disc", and "line" is taken to mean "a circular arc which meets the unit disc at right angles". So a statement like "two points determine a line" can be interpreted as [*] For any two points inside the disc, there is exactly one circular arc which meets the disc at right angles. Indeed, this interpretation5 preserves all of Euclid's postulates except for the parallel postulate. You can see that for a given line and a point not on it, there are an infinite number of parallel (that is, non-intersecting) lines.
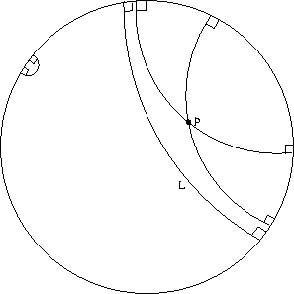
(Note that the distance function is very different within the Poincare disc; in fact the perimeter of the disc is of at infinity. Angles, however, do happen to be preserved.)
The critical point of his interpretation of a non-Euclidean geometry is this: it is embedded in Euclidean geometry! So we are able to prove (within the embedding Euclidean geometry) that the disc-postulates hold (e.g., we can prove the statement [*] above as a theorem about circular arcs in Euclidean geometry). Therefore, if there is any inconsistency in non-Euclidean geometry, then that could be parlayed into some inconsistency of Euclidean geometry. Thus, his interpretation gives a proof that the strange non-Euclidean geometry is as sound as our familiar Euclidean geometry.
- 2927 reads






