What is the most natural way to prove an existential sentence, like "there exists a prime num ber greater than 5"? That's easy you just mention such a number, like 11, and show that it is indeed prime and greater than 5. In other words, once we prove
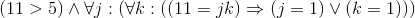
we can then conclude -- using the inference rule ∃Intro that the formula ∃p : ((p> 5) ∧∀j :(∀k : ((p = jk) ⇒ (j = 1) ∨ (k = 1)))) is true. In general, to prove a for mula of the form ∃x :(φ), we show that
φ holds when x is replaced with some particular witness. (The witness was 11 in this example.) The inference rule is 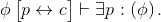 The
notation "φ[v→w]" means the formula φ but with every occurrence of v replaced by w. For example, we earlier wrote down the formula φ[p→11],
and then decided that this was sufcient to conclude ∃p :(φ).
The
notation "φ[v→w]" means the formula φ but with every occurrence of v replaced by w. For example, we earlier wrote down the formula φ[p→11],
and then decided that this was sufcient to conclude ∃p :(φ).
How do you find a witness? That's the difficult part. You, the person creating the proof, must grab a suitable example out of thin air, based on your knowledge of what you want to prove about it. In our previous example, we used our knowledge about prime numbers and about the greater-than relation to pick a witness that would work. In essence, we fgured out what facts needed to be true about the witness for the formula to hold, and used that to guide our choice of witness. Of course, this can easily be more difcult, as when proving that there exists a prime greater than 6971 of the form 4x− 1. (It turns out that 796751 will sufce as a witness here.) Another approach is trial-and-error: Pick some candidate value, and see if it does indeed witness what you're trying to prove. If you succeed, you're done. If not, pick another candidate.
- 1995 reads






