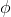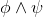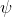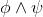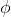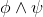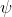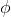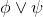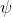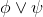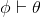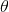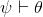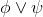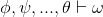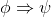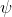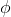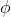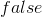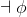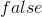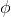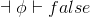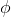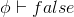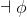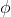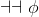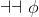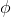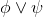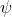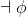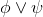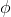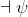|
Abbreviation |
Name |
If you know all of. . . |
. . .then you can infer |
|---|---|---|---|
|
∧Intro |
and-introduction |
|
|
|
|
|||
|
∧Elim |
and-elimination (left) |
|
|
|
and-elimination (right) |
|
|
|
|
∨Intro |
or-introduction (left) |
|
|
|
or-introduction (right) |
|
|
|
|
∨Elim |
or-elimination |
|
|
|
|
|||
|
|
|||
|
⇒Intro |
if-introduction |
|
φ ∧ ψ ∧ . . . ∧ θ ⇒ ω |
|
⇒Elim |
if-elimination (modus ponens) |
|
|
|
|
|||
|
falseIntro |
false-introduction |
|
|
|
|
|||
|
falseElim |
false-elimination |
|
|
|
RAA |
reductio ad absurdum (v. 1) |
|
|
|
reductio ad absurdum (v. 2) |
|
|
|
|
¬Intro |
negation-introduction |
|
|
|
¬Elim |
negation-elimination |
|
|
|
CaseElim |
case-elimination (left) |
|
|
|
|
|||
|
case-elimination (right) |
|
|
|
|
|
As usual, φ, ψ, θ, ω are meta-variables standing for any WFF.
This is by no means the only possible inference system for propositional logic.
ASIDE: This set of inference rules is based upon DiscTete Mathematics with a ComputeT by Hall and O'Donnell (Springer, 2000) and The Beseme Project .
- 2915 reads