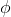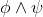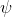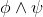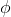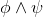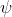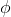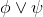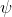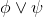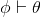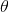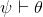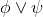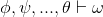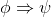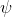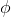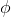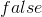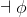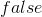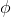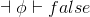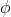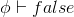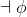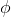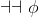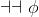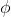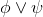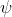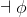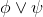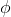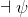Propositional inference rules

You are here

Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/383d4b87-2d7b-454e-99fe-2eaa43eae8ff@20.20

Table 6.2 Our propositional inference rules
Abbreviation	Name	If you know all of. . .	. . .then you can infer
∧Intro	and-introduction	$\phi$	$\phi \wedge \psi$
∧Intro	and-introduction	$\psi$	$\phi \wedge \psi$
∧Elim	and-elimination (left)	$\phi \wedge \psi$	$\phi$
	and-elimination (right)	$\phi \wedge \psi$	$\psi$
∨Intro	or-introduction (left)	$\phi$	$\phi \vee \psi$
	or-introduction (right)	$\psi$	$\phi \vee \psi$
∨Elim	or-elimination	$\phi \vdash \theta$	$\theta$
		$\psi \vdash \theta$
		$\phi \vee \psi$
⇒Intro	if-introduction	$\phi ,\psi ,...,\theta \vdash \omega$	φ ∧ ψ ∧ . . . ∧ θ ⇒ ω
⇒Elim	if-elimination (modus ponens)	$\phi \Rightarrow \psi$	$\psi$
⇒Elim	if-elimination (modus ponens)	$\phi$	$\psi$
falseIntro	false-introduction	$\phi$
falseIntro	false-introduction	$\dashv \phi$
falseElim	false-elimination		$\phi$
RAA	reductio ad absurdum (v. 1)	$\dashv \phi \vdash false$	$\phi$
RAA	reductio ad absurdum (v. 2)	$\phi \vdash false$	$\dashv \phi$
¬Intro	negation-introduction	$\phi$	$\dashv \dashv \phi$
¬Elim	negation-elimination	$\dashv \dashv \phi$	$\phi$
CaseElim	case-elimination (left)	$\phi \vee \psi$	$\psi$
	case-elimination (left)	$\dashv \phi$	$\psi$
	case-elimination (right)	$\phi \vee \psi$	$\phi$
	case-elimination (right)	$\dashv \psi$	$\phi$